מהי הנגזרת של מספר או קבוע

עמוד בהקמה
בשיעור הקודם שבו למדנו מהי הנגזרת ופונקציית הנגזרת, נתקדם ונלמד איך גוזרים ישר שמקביל לציר הx או מאונך לציר הy.

נתחיל מסרטון הסבר קצר מערוץ קרנפים ביוטיוב (תוכן חינמי וחופשי)

לצורך הדוגמא שלנו כאן נתחיל לבחון את פונקציית הישר המאונך לציר הy : y=1

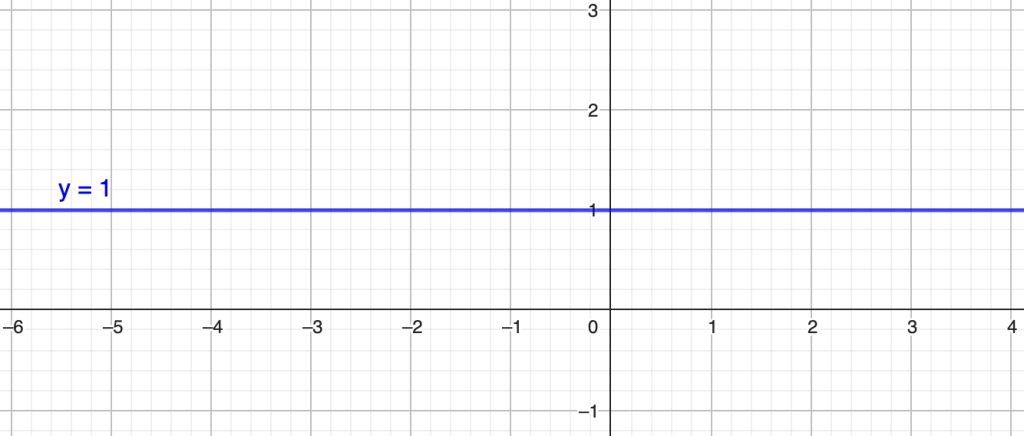
נגזרת של כל קבוע או מספר תהיה שווה לאפס, נכתוב זאת כך:

\(y=f(x)=a \\ y’=f'(x)=0\)

כלומר נגזרת של מספר או קבוע תהיה שווה תמיד לאפס, למשל:
\(y=f(x)=4 \\ y’=f'(x)=0\)
או
\(y=f(x)=-3 \\ y’=f'(x)=0\)

הסבר לנגזרת של מספר:
כלל הגזירה הראשון הוא כלל גזירת מספר, אין כאן יותר מידי דברים מסובכים לדעת, ננסה להסביר את זה בשתי דרכים:
דרך ראשונה – התבוננות וחקירת הגרף. בשלב הזה אנחנו כבר יודעים שהנגזרת היא למעשה פונקציה המתארת את השיפוע של פונקציית המקור, לכן במקרה של ישר המקביל לציר הx, לא משנה כמה נתקדם לאורך ציר הx ערך הפונקציה לא ישתנה (הפונקציה לא תלויה בx) ולכן השיפוע של הפונקציה הוא אפס.