באיזה ידע תשלטו אחרי שתחפרו את העמוד הזה:
- מהו משפט הסינוסים – הגדרה
- הוכחת משפט הסינוסים – זוויות בלבד
- הוכחת משפט הסינוסים – רדיוס מעגל חוסם R
- תכונות הסינוס הבסיסיות
- כמה פתרונות יש למשוואה טריגונומטרית
- תרגול רמה 1
- תרגול רמה 2
- מחשבון משפט הסינוסים
משפט הסינוסים הגדרה:
משפט הסינוסים קובע כי היחס שבין אורך הצלע לסינוס הזווית שמולה שווה לקוטר המעגל (פעמיים רדיוס):
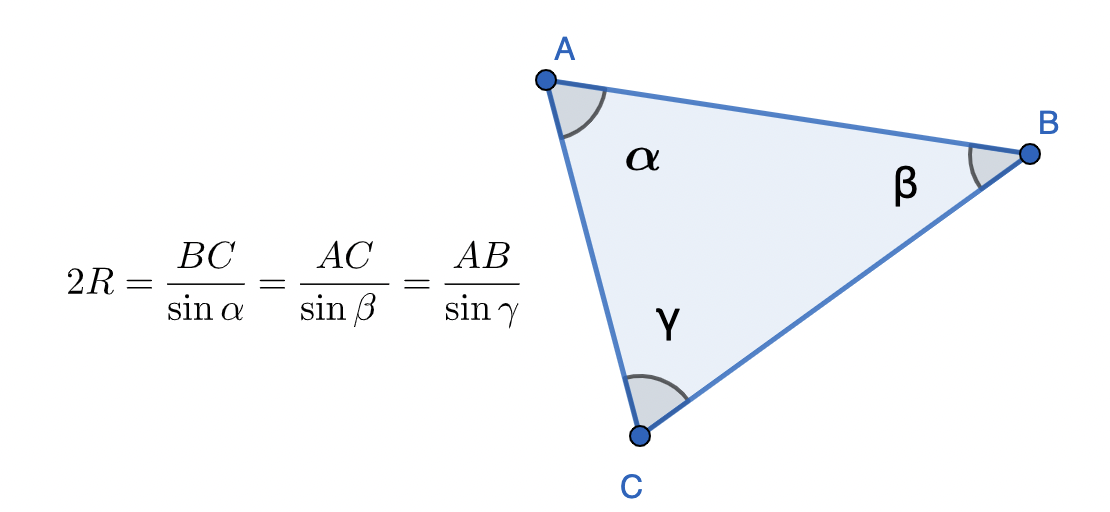
הוכחת משפט הסינוסים:
הוכחת משפט הסינוסים יחסית קלה, הנה שתי הוכחות למשפט הסינוסים:
1.הוכחת משפט הסינוסים ללא היחס של R (רדיוס המעגל החוסם)
\frac{BC}{\sin\alpha }=\frac{AC}{\sin\beta }=\frac{AB}{\sin\gamma }נתבונן במשולש הבא
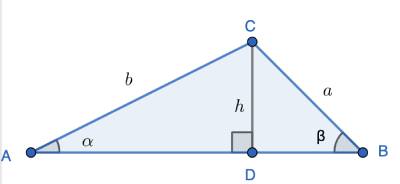
במשולש ABC הורדנו גובה לצלע AB ומכאן יש לנו שני משולשים ישרי זווית ACD ו BCD
כידוע, ההגדרה של פונקציית הסינוס היא היחס שבין הגובה שמול הזווית לבין היתר במשולש ולכן נקבל את היחסים הבאים
במשולש ACD
\sin\alpha = \frac{a}{h} \Rightarrow h=\frac{a}{\sin\alpha}במשולש BCD
\sin\beta = \frac{b}{h} \Rightarrow h=\frac{b}{\sin\beta}מאחר והגובה h שווה בשני המשולשים, נשמר היחס הבא
\frac{a}{\sin\alpha}=\frac{b}{\sin\beta}ומכן ההוכחה למשפט הסינוסים
\frac{BC}{\sin\alpha }=\frac{AC}{\sin\beta }=\frac{AB}{\sin\gamma }2. הוכחת משפט הסינוסים הכוללת את היחס R
- ההוכחה הזאת מתבססת על:
- הוכחת משפט הסינוסים מלמעלה
נתון המעגל הבא
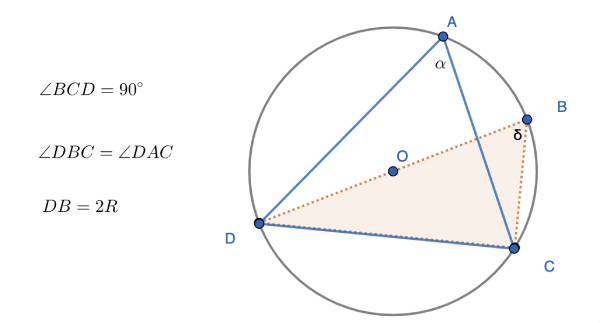
מאחר וזווית BCD הינה שווית ישרה, נקבל את יחס הסינוס:
סינוס שווה ליחס שבין הניצב מול הזוית ליתר
\sin \delta = \frac{DC}{DB}מאחר והקוטר הוא פעמיים הרדיוס, נקבל
DB=2Rומכאן היחס הבא
\sin \delta = \frac{DC}{2R}נבודד את 2R ונקבל את היחס הבא:
2R=\frac{DC}{\sin \delta}מכיוון ששתי זוויות הנשענות על אותה הקשת (מאותו הצד), יש לנו את הזיוויון הבא בזוויות
\delta = \alphaוכמו כן את השוויון בערך הסינוס
\sin \delta = \sin\alphaנכתוב את השיוויון הבא
2R=\frac{DC}{\sin \alpha}קיבלנו את משפט הסינוסים המלא
2R=\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}תכונות בסיסיות של פונקציית הסינוס
כמה תכונות של פונקציית הסינוס שיעזרו לפתור תרגילים מורכבים המצריכים מעבר להצבה מיידית בנוסחאות
- פונקציית הסינוס היא פונקציה אי-זוגית ולכן מקיימת \sin(-\alpha)=-\sin(\alpha)
- פונקציית הסינוס מקיימת \sin(180^\circ – \alpha)= \sin(\alpha)
שאלות תרגול משפט הסינוסים רמה 1
בסוג זה של שאלות, התשובה תהיה תוצאה של שימוש ישיר בנוסחת הסינוסים או המרה אחת בלבד
משפט הסינוסים – שאלת תרגול 1
| שאלה
במשולש הבא נתונים עורכי הצלעות a ו b וכמו כן גודל הזווית α אשר בקודקוד A.
|
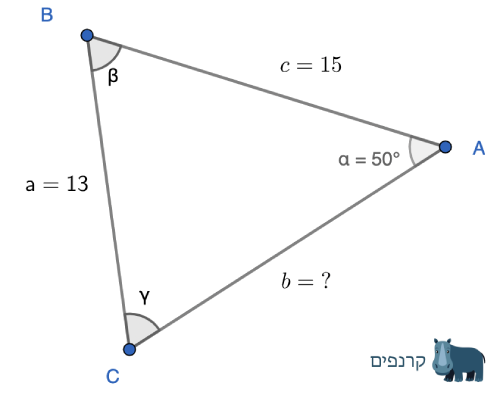 |
פתרון:
ראשית נמצא את גודל זווית 𝛾∠ ע״י הצבה מהירה בנוסחת משפט הסינוסים
\frac{a}{\sin\alpha} = \frac{c}{\sin\gamma}נקבל
\sin\gamma = \frac{c\cdot\sin\alpha}{a} \Rightarrow \angle \gamma = 62.12^\circנחשב את גודל זווית 𝛽 לפי סכום הזוויות במשולש
\beta = 180^\circ – 50^\circ – 62.12^\circ = 67.88^\circכעת נחשב את אורך צלע b ע״י שימוש נוסף במשפט הסינוסים
\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} b =\frac{13 \cdot \sin67.88^\circ}{\sin50^\circ} \Rightarrow b=18.03היקף המשולש הוא כמובן סכום עורכי הצלעות שמצאנו
l=a+b+c=13+18.03+15=46.03משפט הסינוסים – שאלת תרגול 2
| שאלה
במשולש הבא נתונים עורכי הצלעות a ו c וכמו כן גודל הזווית α אשר בקודקוד A.
|
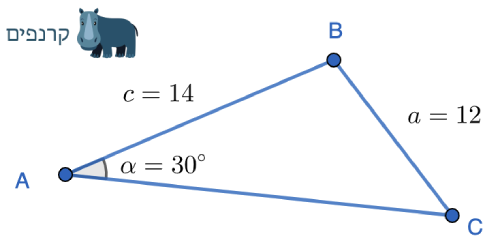 |
פתרון:
ראשית נמצא את גודל זווית BCA∠ ע״י הצבה מהירה בנוסחת משפט הסינוסים
\frac{a}{\sin\alpha} = \frac{c}{\sin(∠BCA)}נקבל
\sin(∠BCA) = \frac{c\cdot\sin\alpha}{a} \Rightarrow \angle \gamma = 35.68^\circנחשב את גודל זווית ∠ABC לפי סכום הזוויות במשולש
\beta = 180^\circ – 30^\circ – 35.68^\circ = 114.32^\circע״י שימוש נוסף במשפט הסינוסים המורחב נחשב את רדיוס המעגל החוסם R
2R=\frac{a}{\sin\alpha} \Rightarrow R= \frac{12}{2\cdot \sin30^\circ}\Rightarrow R= \frac{12}{2\cdot0.5}=12משפט הסינוסים – שאלת תרגול 3
| שאלה
במשולש הבא נתונים עורך הצלעו AC=10 וכמו כן גודל הזווית בקודקוד C.
|
 |
פתרון:
סעיף 1:
ראשית נמצא את גודל זווית CAB∠ ו CBA∠ ע״י שימוש בסכום הזוויות במשולש
180=105+\alpha+2\cdot\alpha \Rightarrow \alpha=\frac{108-105}{3}
נקבל
\alpha=\frac{75}{3}=25^\circ
סעיף 2:
נמצא את עורך הצלע AB ע״י שימוש ישיר בנוסחת משפט הסינוס
\frac{AC}{\sin (\alpha)} = \frac{AB}{\sin(105^ֿ\circ)}נקבל
AB = \frac{AB \cdot \sin (2\cdot \alpha)}{\sin(105^ֿ\circ)}
ומכאן
AB = \frac{10 \cdot \sin(105^ֿ\circ)}{\sin (25^ֿ\circ)}=22.837
באותה הדרך נחשב את אורך הצלע BC
נקבל
BC = \frac{AB \cdot 2 \cdot \sin }{\sin(105^ֿ\circ)}
ומכאן
BC = \frac{22.837 \cdot \sin (50^ֿ\circ)}{\sin(105^ֿ\circ)}=18.109
סעיף 3:
למציאת הרדיוס החוסם את המשולש נשתמש שימוש מהיר בנוסחת הסינוסים
2R=\frac{AC}{\sin\alpha}
מכאן נקבל כי רדיוס המעגל החוסם הוא
R=\frac{AC}{2\cdot\sin\alpha} = \frac{10}{2\cdot0.422}=11.82
את כל שלבי השאלה ניתן לחשב בעזרת מחשבון משפט הסינוסים למטה
משפט הסינוסים – שאלת תרגול 4
נתון המשולש הבא:
אורך צלע אחת 12 והצלע השניה 10. גודל הזוית שמול הצלע הקצרה היא 35 מעלות.
- חשבו את הגדלים האפשריים לזווית שמול הצלע שאורכה 12 סנטימטרים
- בחרו בזווית הגדולה יותר וחשבו את אורך הנותרת.
פתרון:
יש לזכור את תכונת הסינוס
\sin(\alpha)=\sin(180^\circ – \alpha)ניגש לפתרון השאלה:
\frac{12}{\sin\alpha}=\frac{10}{\sin(35^\circ)} \Rightarrow \sin\alpha = \frac{12\cdot\sin(35^\circ)}{12}
ונקבל
\sin\alpha = 0.69
מתוך הידע כי
\sin(\alpha)=\sin(180^\circ – \alpha)
נקבל פתרון ראשון
(\alpha)=\sin^{-1} (0.69) = 43.495^\circ
(\alpha)=180^\circ – 43.495^\circ = 136.505^\circ
כעת נחשב את אורך הצלע החסרה
\gamma = 180^\circ-35^\circ-43.495^\circ=101.505
שימוש בנוסחת הסינוסים יביא ל
A = \frac{10 \cdot \sin(101.505^\circ)}{\sin(35^\circ)}
A = \frac{10 \cdot 0.982}{0.574} = 17.108
מחשבון משפט הסינוסים
הכננו עבורכם מחשבון למשפט הסינוסים, כולל כמה אפשרויות לחישוב ופתרונות מלאים הכוללים הסקות נוספות שניתן להסיק תוך שימוש במשפט הסינוסים (רדיוס מעגל חוסם, היקף ועוד). לנוחיותכם עמוד המחשבון זמין גם כאן – מחשבון משפט הסינוסים (נפתח בעמוד חדש להקלה על השימוש)


