בעמוד הזה נלמד ונתרגל את הנושאים הבאים:
- הסבר על אמצע הקטע
- היכרות עם נוסחת אמצע הקטע
- מחשבון למציאת נקודת אמצע קטע (המחשבון בעמוד חדש)
- תרגול בסיס למציאת אמצע קטע
- תירגול חישוב ומציאת אמצע קטע מתוך שתי נקודות הקצה
באו נתחיל!
אמצע קטע – מבוא:
אמצע הקטע הוא הנקודה שנמצא על ישר המחבר בין שתי נקודות ומחלק את הישר לשני קטעים שווים, המרחק בין הנקודת האמצע לכל אחת מנקודות הקצה של הישר שווה.
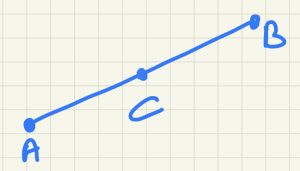
נקודות קצה הקטעע מוגדרות:
A(Xa,Ya). B(Xb,Yb)
נקודת אמצע הקטע C מצויינת כ:
C(Xc,Yc)
הברטוט הבא מתאר את הנקודה C שהיא אמצע הקטע AB:
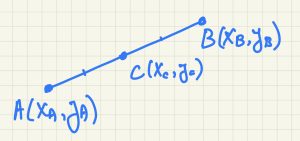
היכרות עם הנוסחה לחישוב אמצע קטע:
לאחר שהבנו את ההתיחסות לקטע AB ולקורדינאטות נקודות הקצה שלו, נוכל לבנות את הנוסחה לחישוב הקורדינטות של נקודה C המחלקת את הישר AB לשני חלקים שווים, כלומר אורכו של הקטע AC שווה לאורכו של הקטע CB.
אם נתונות לנו הקורדינאטות של נקודות A ו B נוכל לחשב את קורדינאטות הנקודה C כך:
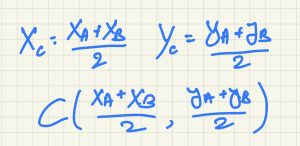
מרגע זה לתרגילים הבאים נשתמש בנוסחה לחישוב אמצע קטע:
C=\left ( \frac{X_{a}+X_{b}}{2},\frac{Y_{a}+Y_{b}}{2} \right )
מחשבון למציאת אמצע קטע
תירגול חישוב ומציאת אמצע קטע מתוך שתי נקודות הקצה:
תרגיל מציאת אמצע קטע #1
מצאו את האמצע בין הנקודות A(3,4) B(5,2)
פתרון:
נסמן את נקודת האמצע באות C ונמצא את ערכי הx והy בנקודה C
מרגע זה לתרגילים הבאים נשתמש בנוסחה לחישוב אמצע קטע:
X_{c}=\frac{X_{a}+X_{b}}{2} = \frac{3+5}{2} = \frac{8}{2} = 4
Y_{c}=\frac{Y_{a}+Y_{b}}{2} = \frac{4+2}{2} = \frac{6}{2} = 3
לסיכום
C(4,3)
תרגיל מציאת אמצע קטע #2
מצאו את האמצע בין הנקודות A(3,-1) B(5,-5)
פתרון:
נסמן את נקודת האמצע באות C ונמצא את ערכי הx והy בנקודה C
מרגע זה לתרגילים הבאים נשתמש בנוסחה לחישוב אמצע קטע:
X_{c}=\frac{X_{a}+X_{b}}{2} = \frac{3+5}{2} = \frac{8}{2} = 4
Y_{c}=\frac{Y_{a}+Y_{b}}{2} = \frac{(-1)+(-5)}{2} = \frac{-6}{2} = -3
לסיכום
C(4,-3)
תירגול חישוב ומציאת אמצע קטע כשידועה נק האמצע ואחת הנקודות:
תרגיל מציאת אמצע קטע כשאחת הנקודות לא ידועה#1
נתונה הנקודה A(1,1) ונקודת האמצע C(3,4), מצאו את הנקודה B
פתרון:
נמצאת קורדינאטות הנקודה B נשתמש באותה הנוסחה, רק שכעת ערכי הקורדינטות Xb ו Xy הן הנעלמים:
3=\frac{X_{a}+X_{b}}{2} = \frac{1+X_{b}}{2}
נכפיל ב2 את האגפים
2\cdot3=1+X_{b}
6=1+X_{b}
נחסיר משני האגפים 1 ונקבל את קורדינאטות Xb
X_{b} = 5
נעשה את אותו התהליך למציאת ערכי Y
4=\frac{Y_{a}+Y_{b}}{2} = \frac{1+Y_{b}}{2}
נכפיל ב2 את האגפים
2\cdot4=1+Y_{b}
8=1+Y_{b}
נחסיר משני האגפים 1 ונקבל את קורדינאטות Yb
Y_{b} = 7
לסיכום
B(5,7)


