אחוזים

מה בשיעור?

1. הסבר על מושג אחוז % והמחשה גרפית של האחוז
2. איך עוברים משברים פשוטים, מדומים או מעורבים לאחוזים
3. איך עוברים משבר עשרוני לאחוזים
4. תרגול מפורט –
   1. מעבר משבר לאחוזים
   2. מעבר משבר עשרוני לאחוזים
   3. כמה הוא אחוז מתוך?
   4. שאלות מילוליות בנושאי אחוזים
5. רשימת דפי עבודה לקרנפים מתרגלים

מהו אחוז?

אחוז הוא אחת הדרכים להציג חלק מתוך שלם

אחוז אחד הוא בעצם שבר של 1 חלק מאה

הגדרה גרפית של אחוז אחד:

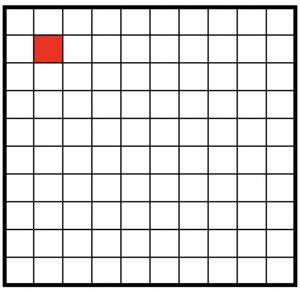
דמיינו שיש לכם טבלה ובה 100 תאים, כמו הטבלה הבאה:

מכיוון שבטבלה 100 תאים ( 10 שורות על 10 עמודות) אם נצבע תא אחד בטבלה בעצם נצבע חלק אחד מתוך 100 ולכן בעצם נצבע אחוז אחד מתוכה.

בואו נראה כמה יצוגים של אחוזים בטבלה:

1%

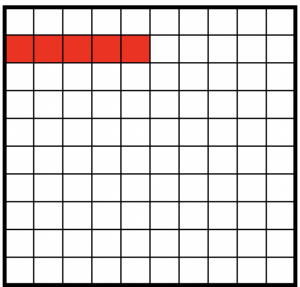
5%

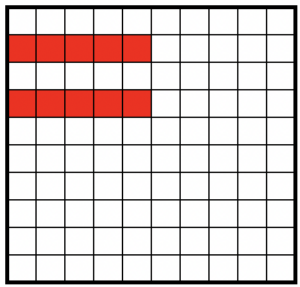
10%

חשוב לציין שכשאנחנו באים לצבוע אחוזים בטבלה, לא משנה באיזה תא נבצע את האחוז, הקו המנחה אותנו הוא מספר התאים שצבענו.

הכנו לכם דף ובו 9 טבלאות 100 ריקות להדפסה, תוכלו לתרגל בו צביעת אחוזים, הדפיסו את הדף וצבעו 5%, 12% , 17%, 24% וכן הלאה

איך עוברים משבר פשוט לאחוזים

כדי לעבור משבר פשוט לאחוזים, נכפיל את המונה של השבר ב100 ונצמצם, התוצאה תהיה האחוזים שאותם מייצג השבר, למשל

כמה אחוזים מייצג \(\frac{1}{4}\)
כאמור כדי לעבור משבר לייצוג באחוזים, נכפיל את המונה ב100 ונמצמצם
\(\frac{1 \cdot 100}{4} = \frac{100}{4}\)
אפשר לצמצם את 100 ב 4 וכך נקבל
\(\frac{100}{4} = 25\)
לכן השבר \(\frac{1}{4}\) ניתן לייצוג כ \(25\%\)

דוגמא נוספת

כמה אחוזים מייצג \(\frac{2}{7}\)
נכפיל את המונה ב100 ונמצמצם
\(\frac{2 \cdot 100}{5} = \frac{200}{5}\)
אפשר לצמצם את 200 ב 5 וכך נקבל
\(\frac{200}{5} = 40\)
לכן השבר \(\frac{2}{5}\) ניתן לייצוג כ \(40\%\)

איך עוברים משבר עשרוני לאחוזים

המעבר לאחוזים משבר עשרוני הוא פשוט ביותר, כל מה שצריך לעשות הוא לכפול את השבר העשרוני ב100, התוצאה תהיה האחוזים שהוא מייצג.

לדוגמא:
כמה אחוזים מיוצגים ב 0.4
כאמור, יש לכפול את 0.4 ב100
\(0.4 \cdot 100 = 40 \%\)

דוגמא נוספת:
כמה אחוזים מיוצגים ב 0.27
כאמור, יש לכפול את 0.27 ב100
\(0.27 \cdot 100 = 27 \%\)

דוגמא נוספת:
כמה אחוזים מיוצגים ב 0.658
כאמור, יש לכפול את 0.658 ב100
\(0.658 \cdot 100 = 65.8 \%\)

כדאי להבין כמה דברים:

1. מעבר משבר עשרוני לאחוזים הוא מכפלה ב100
2. אם יש לנו מספר שהוא מספר אחד אחרי הנקודה, כמו 0.3 , אפשר לכתוב אותו בראש כ 0.30 וכאשר יש לנו שבר עשרוני שבו 2 ספרות אחרי הנקודה, הספרות הן בעצם האחוז 0.30 הם בעצם 30%
3. אם יש לנו מספר ובו יותר משתי ספרות אחרי הנקודה, הכפלה ב100 בעצם מעבירה את הנקודה 2 מקומות ימינה ואנחנו מקבלים את האחוזים שאותו שבר מייצג, למשל 0.6788 נזיז את הנקודה 2 מקומות ימינה ונקבל את מספר האחוזים 67.88%

סוגי שאלות בנושאי אחוזים:

1. כמה אחוזים הם שבר פשוט/מדומה/מעורב?
2. כמה אחוזים הם שבר עשרוני
3. כמה הם %x מתוך משהו
4. שאלות מילוליות – מציאת גודל הנחה או מחיר אחרי הנחה

נפתור כמה דוגמאות:

כמה אחוזים הם שבר פשוט/מדומה/מעורב?

שאלה 1

כמה אחוזים הם \(\frac{3}{5}\)
בתחילת העמוד הסברנו שכדי לעבור משבר פשוט לאחוזים יש להכפיל ב100 ולצמצם במידת האפשר
\(100 \cdot \frac{3}{5} = \frac{100 \cdot 4}{5}=\frac{300}{5}\)
כעת נצמצם ונקבל
\(\frac{300}{5}=\frac{60 \cdot 5}{5}=60 \%\)

שאלה 2
כמה אחוזים הם \(2 \frac{3}{4}\)
ראשית נעבור משבר מעורב לשבר מדומה
\(2 \frac{3}{4} = \frac{2 \cdot 4 + 3}{4} = \frac{11}{4}\)
כעת נכפיל את השבר ב100
\(100 \cdot \frac{11}{4} = \frac{100 \cdot 11}{4}=\frac{1100}{4}\)
כעת נצמצם ונקבל
\(\frac{1100}{4}=\frac{1100 \cdot 4}{4}=275 \%\)
באופן כללי, שבר מעורב ניתן להפריד, כאשר כל שלם שווה ל 100% ואילו את השבר ממשיכים לפתור כרגיל
במקרה שלנו
\(2=200%\)
\(\frac{3}{4} = 75 \%\)
ולכן
\(2 \frac{3}{4} = 200 \% + 75 \%= 275\%\)

שאלות מסוג : כמה אחוזים הם שבר עשרוני?

כמו השאלות מסוג המרת שברים רגילים לאחוזים, כאן נמיר שברים עשרוניים
הכלל הפשוט שנאחנו צריכים לעקוב אחריו הוא שכדי להמיר משבר עשרוני לאחוזים אנחנו בעצם כופלים ב100

דוגמא 1:
כמה אחוזים הם 0.4?
כאמור, פשוט נכפול ב100
\(0.4 \cdot 100= 40 \%\)
צורה נוספות להסתכל על ההמרה הפשוטה הזאת היא ע״י הזזת הנקודה 2 מקומות ימינה
אז נוכל לכתוב את השבר העשרוני כשיש לו לפחות שני מקומות אחרי הנקודה, לכן 0.4 יהיה בעצם 0.40
\(0.40 \cdot 100 = 40 \%\)

דוגמא 2:
כמה אחוזים הם 1.32?
כמו בדוגמאות הקודמות, פשוט נכפול את השבר העשרוני ב100
\(1.32 \cdot 100 = 132\%\)

דוגמא 3:
כמה אחוזים הם 0.555?
נכפול את השבר העשרוני ב100
\(0.555 \cdot 100 = 55.5\%\)

שאלות מסוג כמה הם %x מתוך משהו

אלו הן השאלות המתקדמות יותר, מה שנקרא להן שאלות מהחיים
את השאלות האלה נפתור בעזרת מכפלת האחוזים בX ונחלק ב100,
בואו נתרגל קצת

דוגמא 1:
כמה הם 30% מתוך 60?
פתרון
נכפיל את 30 ו60 ונחלק ב100
\(X = \frac{30 \cdot 60}{100} = \frac{1800}{100} = 18\)

נפתור דוגמא נוספת מהסוג הזה
דוגמא 2:
כמה הם 45% מתוך 200?
פתרון
נכפיל 45 ב200 ונחלק ב100
\(X = \frac{45 \cdot 200}{100} = \frac{9000}{100} = 90\)

 

שאלות מילוליות – מציאת גודל הנחה או מחיר אחרי הנחה

בשאלות מהסוג הזה, נישאל לרוב מה הוא המחיר אחרי הנחה מסויימת או מה גודל ההנחה שנקבל

דוגמא 1:

יואב רכש בובת פופ של מוטי הקוסם, המחיר המקורי של הבובה היה 50 שקלים, לכבוד חג הפורים, כל בובות הפופ נמכרו בהנחה של 10%, כמה עלתה בובת הפופ של מוטי הקוסם?

פתרון

ראשית נצטרך להבין מהי משמעו הנחה. מחיר רגיל הוא למעשה 100% מהמחיר המקורי (כשאנחנו כופלים 100% במשהו אנחנו בעצם כופלים ב1) לכן אם ישנה הנחה של 10%, אנחנו בעצם מחסרים מ100% 10% ואנחנו מקבלים 90%, כעת כדי לדעת מה מחיר הבובה, נכפול את המחיר הרגיל שלה ב90 ונחלק ב100
\(מחיר = \frac{(100-10) \cdot 50}{100}\)
נמשיך בפתרון
\(מחיר = \frac{90 \cdot 50}{100}\)
ובשלב האחרון
\(מחיר = \frac{4500}{100} = 45_{ש״ח}\)

 

דוגמא 2:
סיוון הגיע לחנות כלי הכתיבה ״אפרים הכותב״, היא רכשה ציוד לתחילת שנת הלימודים בעלות של 150 שקל, על כל המוצרים בחנות ישנה הנחה של 10% והנחה נוספת של 5% בקניה מעל 100 שקלים. כמה שילמה סיוון בקופה?

פתרון

מכיוון שיש לנו 2 הנחות, הנחה ראשונה על המוצרים עצמם ונחה נוספת על בקופה, אנחנו נכפול פעמיים בגודל ההנחה. שימו לב שאין כאן סכום של אחוזי ההנחה, כלומר הנחה של 10%+5%.

נחשב את עלות המוצרים אחרי ההנחה הראשונה של 10%
\( X_{1} = \frac{150 \cdot (100-10)}{100} = \frac{150 \cdot 90}{100} \)
המחיר לאחר ההנחה הראשונה
\( X_{1} = \frac{13500}{100} = 135\)
כעת נחשב את המחיר לאחר ההנחה הנוספת של 5%
\( X = \frac{135 \cdot (100-5)}{100} = \frac{135 \cdot 95}{100} \)
המחיר לאחר ההנחה הראשונה
\( X = \frac{12,825}{100} = 128.5\)
המחיר הסופי הוא 128.5 שקלים

 

שאלה 3:

ארז קנה בחנות הביגוד קרנף חולצה חדשה לחג החנוכה. מחיר החולצה מקורי היה 80 שקלים, בקופה גילה ארז שיש הנחת חג ושילם עבור החולצה 72 שקלים בלבד. מה גודל ההנחה שקיבל ארז?

פיתרון

אנחנו יודעים כאן מה היה המחיר המקורי והמחיר החדש, ניצור משוואת אחוזים כמו בשאלות קודמות ונמצא את גודל ההנחה x

\(72 = \frac{(100-x) \cdot 80}{100}\)
נכפול את שני האגפים ב 100
\(100 \cdot 72 = (100-x) \cdot 80\)
נמשיך בפתיחת הסוגריים
\(7200 = 8000 – 80x\)
נחלק את שני האגפים ב10
\( 720 = 800 -8x \)
נעביר אגפים ונכתוב
\(8x = 800-720 = 80 \)
נחלק את שני האגפים ב8 ונקבל את גודל ההנחה
\(x = 80:8 = 10 \%\)

 

דפי עבודה באתר בנושאי שברים:

לכיתה ה׳-ו׳

• חישוב שברים מעורבים – אתגר
• חישוב שברים מדומים – אתגר

לכיתה ו׳ ומעלה

• תרגול המחשת ערכו של האחוז – חלק 1
• תרגול המחשת ערכו של האחוז – חלק 2
• תרגול המחשת ערכו של האחוז – חלק 3
• חישוב אחוז מתוך שלם
• משחק חישוב אחוזים לכיתה ו׳ – ראשון
• משחק חישוב אחוזים לכיתה ו׳ – שני
• מבחן אמצע לכיתה ו בנושא אחוזים
• שאלות מילוליות באחוזים לכיתה ו׳ – חלק ראשון
• שאלות מילוליות באחוזים לכיתה ו׳ – חלק שני
• אחוזים חלק ראשון
• אחוזים חלק שני