העמוד בבניה
הי בעמוד הבא נכסה את נושא הפרבולה, החל ממושגי מבוא ועד לפתרון שאלות פרבולה המופיעות בבחינת הבגרות 3 יחידות. בכל סעיף נסביר בעזרת תרגילים ופתרונות וידאו
בתפריט הבא תוכלו לדלג למקום המתאים לכם:
- היכרות עם הפרבולה
- זיהוי הפרמטרים של הפרבולה
- פרבולה בוכה – פרבולה עם ערך מקסימום
- פרבולה צוחקת – פרבולה עם ערך מינימום
- מציאת נקודת הקיצון של הפרבולה
- ציר הסימטריה של הפרבולה
- מציאת נקודות החיתוך של הפרבולה עם ציר ה-x
- משמעות גרפית של פרבולה עם 0,1,2 נקודות חיתוך עם ציר ה-x
- מציאת נקודות החיתוך של הפרבולה עם ציר ה-y
- מציאת נקודות החיתוך של פרבולה עם ישר y=a
- מציאת נקודות החיתוך של פרבולה עם ישר y=ax+b
- מציאת נקודות החיתוך בין שתי פרבולות
- איך גוזרים פונקציה של פרבולה
- שאלות חקירת פרבולה מתוך שאלון 35381/802
היכרות עם הפרבולה
משוואת או פונקציית הפרבולה נראית כך:
\(f(x)=ax^2+bx+c\)
כאשר a,b,c, הם מקדמי הפאבולה
המקדמים c ו b יכולים להיות כל מספר (חיובי שלילי או אפס)
ואילו המקדם a צריך להיות שונה מ אפס כדי שתהיה לנו פרבולה
אם a=0 נקבל בעצם משוואה של ישר ולא משוואה של פרבולה
\(f(x)=0x^2+bx+c = bx+c\)
אם מביט לרגע במשוואת הישר
\(y=mx+b\)
נוכל לראות את הדמיון בין משוואת הישר ומשוואת הפרבולה ונראה שהתוספת למשוואת הפרבולה היא למעשה האיבר החדש של ריבוע x
\(y={\color{Orange} ax^2}+bx+c\)
כמה דוגמאות למשוואה של פרבולה
\(a=1,b=2,c=3 => f(x)=x^2+2x+3\) \(a=2,b=1,c=4 => f(x)=2x^2+x+4\) \(a=-2,b=3,c=-1 => f(x)=-2x^2+3x-1\) \(a=-1,b=2,c=0 => f(x)=-x^2+2x\) \(a=-1,b=0,c=2 => f(x)=-x^2+2\)\(a=2,b=0,c=0 => f(x)=2x^2\)
המשותף לכולן הוא קיום של איבר x בריבוע
מושגים נוספים:
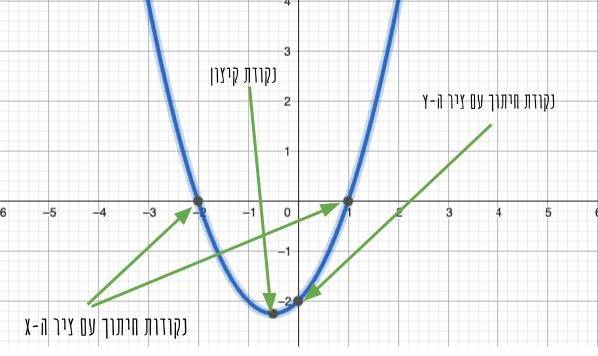
- קודקוד הפרבולה – הנקודה שבה הפרבולה משנה כיוון- מעלייה לירידה או מירידה לעלייה
- נקודות חיתוך עם ציר הx – נקודות שבהן ערך הy של הפרבולה הוא אפס. ישנם שלושה מצבים נפוצים, 2 נקודות חיתוך עם ציר הx, נקודת חיתוך אחת עם ציר הx או אפס נקודות חיתוך עם ציר הx
- נקודת חיתוך עם ציר הy – לפרבולה תהיה תמיד נקודת חיתוך אחת עם ציר הy. את ערך הy הזה נקבל כאשר x=0
זיהוי הפרמטרים של הפרבולה
לימדנו למעלה שלפרבולה ישנם שלושה מקדמים a,b,c, אלו הם מקדמי הפרבולה
המקדם a הוא המספר המופיע לפני איבר ה-x הריבועי
המקדם b הוא המספר המופיע לפני איבר ה-x
המקדם c הוא המספר החופשי
כמו כן אמרנו שהמקדם a אינו יכול להיות אפס מכיוון שאז אין לנו פרבולה אלא פונקציה של קו ישר (פונקציה ממעלה ראשונה) ואילו המקדמים b ו c יכולים להיות שווים לאפס
מה הם מקדמי הפרבולה
\(f(x)=2x^2+4x+6\)מקדמי הפרבולה הם:
\(a=2, b=4, c=6\)
מה הם מקדמי הפרבולה
\(f(x)=-x^2+2x-1\)מקדמי הפרבולה הם:
\(a=-1, b=2, c=1\)
מה הם מקדמי הפרבולה
\(f(x)=-3x^2+2\)מקדמי הפרבולה הם:
\(a=-3, b=0, c=2\)
מה הם מקדמי הפרבולה
\(f(x)=(x+3)(x-2)\)במקרה הזה נצטרך לפתוח סוגריים בעזרת חוק הפילוג:
\(f(x)=x(x-2)+3(x-2)\)
נמשיך
\(f(x)=x^2-2x+3x-6\)
נסכום את המקדמים ונקבל את משוואת הפרבולה
\(f(x)=x^2+x-6\)
מקדמי הפרבולה הם:
\(a=1, b=1, c=-6\)
פרבולה בוכה – פרבולה שיש לה נקודת מקסימום
את הפרבולה הבוכה נוכל לאתר כאשר המקדם a בעל ערך שלילי למשל בפונקציה הבאה a=-1 ולכן שלילי
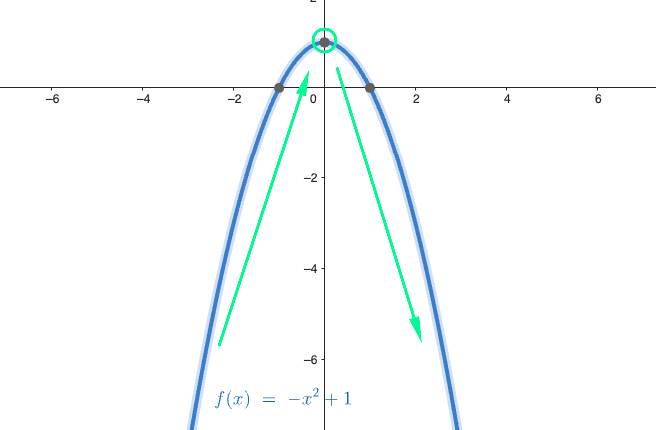
\(f(x)=-x^2+1\)
צורת הפרבולה תהיה קמורה או בוכה
לפרבולה בוכה יש נקודת מקסימום, אנחנו רואים שהיא עוברת מעליה לירידה בנקודת הקודקוד ולכן זוהי נקודת מקסימום, הביטו בסרטוט הבא:
פרבולה צוחקת – פרבולה שיש לה נקודת מינימום
את הפרבולה הצוחקת נוכל לאתר כאשר המקדם a בעל ערך חיובי למשל בפונקציה הבאה a=1 ולכן חיובי
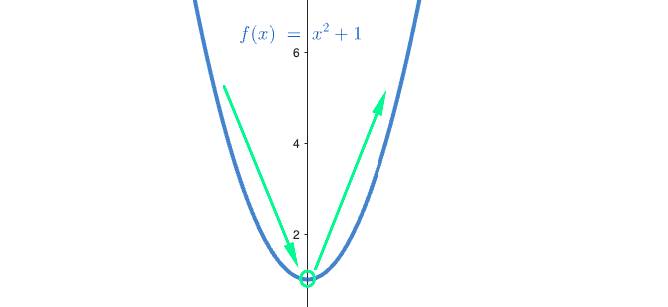
\(f(x)=x^2+1\)
צורת הפרבולה תהיה קעורה או צוחקת
לפרבולה צוחקת יש נקודת מינימום, אנחנו רואים שהיא עוברת מירידה לעליה בנקודת הקודקוד ולכן זוהי נקודת מינימום, הביטו בסרטוט הבא:
מציאת נקודת הקיצון של הפרבולה
אז בסעיף הקודם הבחנו בין שתי צורות של פרבולה
- פרבולה צוחקת – יש לה נקודת מינימום
- פרבולה בוכה – יש לה נקודת מקסימום
כעת נראה איך נוכל למצוא את הקורדינאטות של הנקודה הזאת.
ישנן שתי דרכים למצוא את הקודקוד של הפרבולה:
- ע״י נוסחה למציאת ערך ה-x והצבתו בפונקציה לקבלת ערך ה-y
- גזירה של פונקצית הפרבולה, השוואה לאפס כדי למצוא את ערך ה-x בנקודת הקיצון ולאחר מכן הצבה של ערך ה-x בפרבולה וקבל ערך ה-y בנקודת הקיצון
בשלב הזה נראה את השימוש בנוסחה למציאת ערך ה-x של נקודת הקיצון בפרבולה.
הנוסחה למציאת x קודקוד
\(x_{קודקוד}=-\frac{b}{2a}\)
כאשר b ו a הם מקדמי הפרבולה אותם נציב בנוסחה
בואו נראה כמה דוגמאות
מצאו את ערך ה-x בנקודת הקודקוד של הפרבולה הבאה
\(f(x)=x^2+4x-5\)
ראשית נמצא את ערכי המקדמים bו a
a=1 , b=4 ונציב אותם בנוסחה למציאת x קודקוד
\(x_{קודקוד}=-\frac{b}{2a}=-\frac{4}{2\cdot1}=-2\)
לכן
\(x_{קודקוד}=-2\)
מצאו את ערך נקודת הקיצון של הפונקציה הבאה וקבעו את גוסה (מינימום או מקסימום
\(f(x)=-3x^2+6x-4\)
כמו בשאלה הראשונה, נאתר תחילה את המקדמים של הפרבולה
a=-3 ו b=6
נציב אותם בנוסחה למציאת x קודקוד
\(x_{קודקוד}=-\frac{b}{2a}=-\frac{3}{2\cdot(-3)}=1\)
לכן
\(x_{קודקוד}=1\)
כעת נציב את הנקודה x=1 בפונקציית הפרבולה ונקבלת את ערך ה y בנקודת הקיצון
\(f(x=1)=-3\cdot1^2+6\cdot1-4\)
נכתוב
\(y_{קודקוד}=-3+6-4=-1\)
נקבל
\(y_{קודקוד}=-1\)
ולכן נקודת הקודקוד היא
(1,-1)
משמצאנו את שיעורי נקודת הקיצון נקבע את אופיה צוחקת או בוכה
המקדם a של הפרבולה הוא a=-3 ולכן הפרבולה צוחקת
לפרבולה צוחקת יש נקודת מינימום
ציר הסימטריה של הפרבולה
ציר הסימטריה של הפרבולה הוא ציר שאם נקפל לאורכו את הפרבולה נקבל את אותם ערכי ה-y עבור נקודות הנמצאות במרחק שווה מציר הסימטריה.
ציר הסימטריה של פרבולה הוא ישר מהסוג x=m.
כאשר נתונה משוואת הפרבולה, הערך של m הוא למעשה ערך הנקודה \(X_{קודקוד}\)
נושא אותו למדנו זה עתה למעלה, למשל
נציב את ערכי המקדמים a=1 ו b=6 בנוסחה למציאת ערך הx של קודקוד הפרבולה
\(x_{קודקוד}=-\frac{b}{2a}=-\frac{6}{2\cdot1}=-3\)
ולכן ציר הסימטריה של הפרבולה הוא
x=-3
איך גוזרים פונקציית פרבולה
שאלות חקירת פרבולה מתוך שאלוני 35381/802
חקירת פרבולה שאלה 1 👀 שאלון 802/35381 חורף 2020 מועד א׳
שאלה 1 פרבולה 👀 שאלון 802/35381 קיץ 2020 מועד ב׳
שאלה 1 פרבולה 👀 שאלון 802/35381 קיץ 2020 מועד א׳
שאלת חקירת פרבולה 👀 שאלון 802/35381 חורף 2021 מועד א׳
שאלת פרבולה 👀 שאלון 802/35381 חורף 2020 מועד נבצרים