בעמוד הזה נלמד על חקירת. פונקציית פלינום. פולינום הוא פונקציה בעל איברים רבים, דוגמאות לפולינום:
f(x)=6x^2+2x+5
f(x)=x^3+\frac(x)(5)
f(x)=x^2(5-7x^3)
וכן הלאה
מה נתבקש למצוא בשאלות חקירת הפולינום?
- תחום הגדרה
- נקודות חיתוך עם הצירים
- נקודות קיצון
- מציאת אופי נקודות הקיצון (מקסימום או מינימום)
- תחומי העלייה והירידה
- שרטוט של הפונקציה
נחקור בצורה מלאה את הפונקציות הבאות:
בואו נתחיל בתירגול
חקירת הפולינום f(x) = x^3+2x^2
מציאת תחום הגדרה – מכיוון שאין לנו הגבלות על הפונקציה, תחום ההגדרה הוא כל x
מציאת נקודות החיתוך עם הצירים:
כדי למצוא את נקודות החיתוך עם הצירים, נשוואה את הפונקציה ל 0, כך:
x^3+2x^2=0
נוציא גורם משותף
x^2(x+2)=0
מכאן יש לנו שני ערכים של x שפותרים את המשוואה
x=0
ו
x+2=0 \rightarrow x=-2
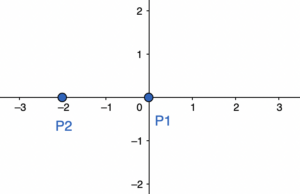
נסמן את הנקודות על הצירים
נכתוב את נקודות החיתוך עם הצירים שמצאו
P1(0,0) , P2(-2,0)
מציאת נקודות קיצון לפולינום
כדי למצוא את נקודות הקיצון של הפולינום נגזור את הפונקציה פעם אחת (הסברים על גזירת פולינום אפשר למצוא כאן)
f(x) = x^3+2x^2
אז
f'(x) = 3x^2+4x
כעת נשוואה את הנגזרת הראשונה לאפס ונמצא את הנקודות החשודות כנקודות קיצון
3x^2+4x=0
נוציא גורם משותף
x(3x+4)=0
הנגזרת מתאפסת עבור הנקודות
x=0
3x+4=0 \rightarrow x=-\frac{4}{3} = -1.333
נמצא את ערכי הפונקציה בנקודות החשודות כנקודות קיצון
f(0) = 0 \rightarrow A(0,0)
f(-\frac{4}{3}) = (-\frac{4}{3})^3 + 2(-\frac{4}{3})^2 = 1.185 \rightarrow B(-1.33 , 1.185)
נוסיף לשרטוט את מיקום המקודות החשודות כנק׳ קיצון
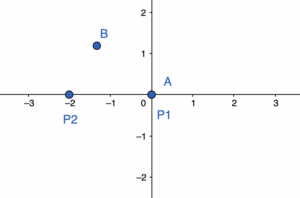
*** נקודה A ו P1 הן אותה הנקודה.
***מתוך מיקום נקודות הקיצון אנחנו כבר יכולים להסיק שנקודה B נקודת מקסימום ואילו נקודה A היא נקודת מינימום, בגלל שנקודה B נמצאת מעל נקודה A
מציאת סוג נקודת הקיצון:
ישנן כמה שיטות לקביעת האופי של נקודת הקיצון, על חלקן הגדול עברנו בשיעור המלמד על מציאת נקודות קיצון
כאן אנחנו נשתמש בהצבה בטבלה של ערכי הנגזרת בסביבת נקודות הקיצון
נמצא את ערך הנגזרת בנקודות סמוכות לנקודות החשודות כנקודות קיצון
אנחנו מתקדמים (x הולך וגדל) משמאל לימין
אם אנחנו רואים שערך הנגזרת עובר מעלייה לירידה, כמו בנקודהx=-1.33 אנחנו יכולים לקבוע שהנקודה היא נקודת מקסימום
אם אנחנו רואים שערך הנגזרת עובר מעליה לירידה כמו בנקודה x=0 אנחנו יכולים לקבוע שהנקודה היא נקודת מינימום
| 1 | 0 | 1- | 1.33- | 2- | |
| 7 | 0 | 1- | 0 | 4 | נגזרת |
| עולה | יורדת | עולה | הפונקציה עולה או יורדת | ||
| מינימום | מקסימום | סוג הנקודה |
מציאת תחומי עליה וירידה:
הטבלה שיצרנו בסעיף הקודם אומרת לנו בדיוק מהם תחומי העלייה והירידה של הפונקציה, נסמן אותם בשרטוט, כאשר בתחום הכחול הפונקציה נמצאת בעלייה ואילו בתחום הירוק הפונקציה נמצא בירידה
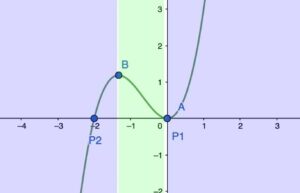
ונכתוב אותם בצורה מתמטית
תחום עלייה – -1.33<x<0
תחום ירידה – x<-1.33 , x>0
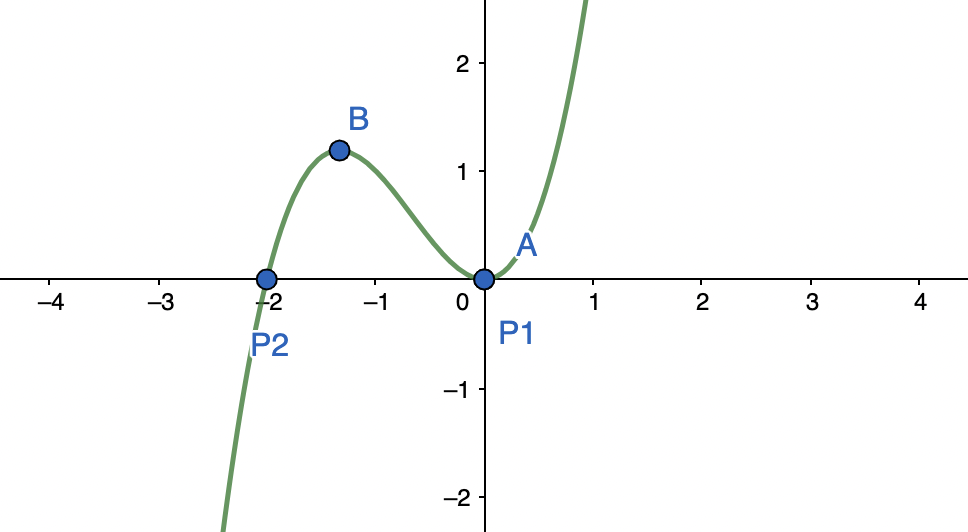
שרטוט של הפונקציה
יש לנו כבר מספיק מידע כדי לשרטט את גרף הפונקציה. מומלץ בכל שלב של החקירה להוסיף נקודות על הגרף ולבנות את גרף הפונקציה תוך כדי התקדמות מסעיף לסעיף.
חקירת הפולינום f(x) = x^4 – 4X^2
תחום הגדרה : אין שום מגבלות על הפונקציה או נקודות שבהן הפונקציה לא מוגדרת, לכן הפונקציה מוגדרת לכל x.
מציאת נקודות חיוך עם ציר ה x:
נשווה את הפונקציה לאפס
f(x) = x^4 -4X^2 =0
נוציא x בריבוע כגורם משותף
f(x) = x^2(x^2 – 4) =0
נמצא את נקודות החיתוך עם ציר ה x
x_1=0 \rightarrow p_1(0,0)=0
נקודות חיתוך נוספות
x^2-4=0 \rightarrow x^2=4
יש לנו שני פתרונות אפשריים נוספים
x_2=2 \rightarrow p_2(2,0)
ו
x_3=-2 \rightarrow p_3(-2,0)
לסיכום, אלה נקודות החיתוך של הפונקציה עם הצירים
P_1(0,0) , P_2(2,0) , P_3(-2,0)
טיפ: אפשר לכתוב את הפונקציה גם כך
x^2(x^2-4) = 0
אנחנו יכולים לראות שהחלק בסוגריים אפשר להמיר בנוסחת הכפל המקוצר
a^2-b^2 = (a-b)(a+b)
ולכן אפשר לכתוב את הפונקיצה כ
x^2(x+2)(x-2)=0
ומכאן פתרונות המשוואה, שהם נקודות החיתוך פשוטים להסקה
נצייר את נקודות החיתוך על הצירים ונמשיך לשלב הבא:
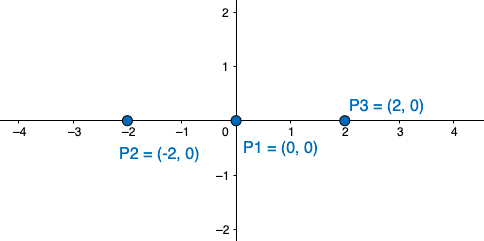
מציאת נקודות החשודות כקיצון:
למציאת נקודות החשודות כקיצון, יש לגזור את הפונקציה ולהשוות אותה ל אפס:
f(x) = x^4 – 4X^2
אז
f'(x)=4x^3 -8x
נשווה לאפס ונמצא את הנק׳ החשודות כקיצון
4x^3 – 8x = 0
נוציא 4x גורם משותף
4x(x^2-2) =0
נשתמש בנוסחת הכפל המקוצר ונמצא את פתרונות המשוואה
4x(x-\sqrt2)(x+\sqrt2)
מכאן שנקודות הקיצון נתונות כאן:
x_1=0 , x_2=\sqrt2 , x_3=-\sqrt2
נמצא את ערכי הפונקציה בנקודות החשודות כקיצון
f(0)=0 \rightarrow A(0,0)
f(\sqrt2)=-4 \rightarrow C(\sqrt2,-4)
f(-\sqrt2)=-4 \rightarrow B(-\sqrt2,-4)
נוסיף את הנקודות החשודות כקיצון למערכת הצירים
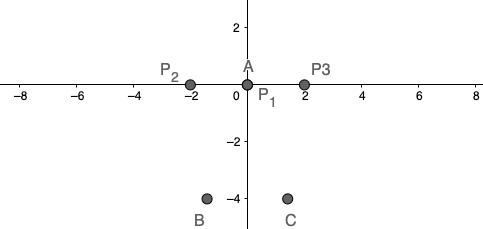
מציאת אופי נקודות הקיצון (מקסימום או מינימום):
נמלא טבלה המכילה את ערכי הנגזרת הראשונה בקרבת הנקודות החשודות כקיצון ונקבע :
נקודת מקסימום, אם אנחנו רואים שערך הנגזרת בסביבת הנקודה החשודה משתנה מחיובי לשלילי (עובר מעליה לירידה)
נקודת מינימום, אם אנחנו רואים שערך הנגזרת בסביבת הנקודה החשודה משתנה משלילי לחיובי (עובר מירידה לעליה)
| 2 | -\sqrt2 | 1 | 0 | 1 | -\sqrt2 | 2- | |
| 16 | 0 | 4- | 0 | 4 | 0 | 16- | נגזרת |
| עלייה | ירידה | עלייה | ירידה | הפונקציה עולה או יורדת | |||
| מינימום | מקסימום | מינימום | סוג הנקודה |
אנחנו יכולים עכשיו לקבוע את סוג הנקודות:
בנקודה B(-\sqrt2,-4) עוברים מירידה לעלייה ולכן היא נקודת מינימום
בנקודה A(0,0) עוברים מעלייה לירידה ולכן היא נקודת מינימום
בנקודה C(\sqrt2,-4) עוברים מירידה לעלייה ולכן היא נקודת מינימום
קביעת תחומי עלייה וירידה:
מתוך הטבלה נוכל לציין את תחומי העלייה והירידה של הפונקציה, נסמן אותם על הגרף ונכתוב ייצוג מתמטי שלהם:
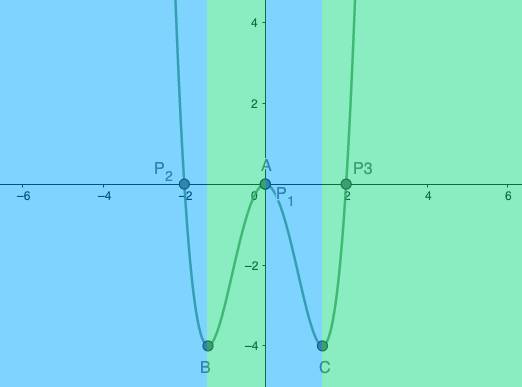
בתחומי הצבע הירוק אנחנו רואים שהפונקציה נמצאת תמיד בעלייה
בתחומי הצבע הכחול אנחנו רואים שהפונקציה נמצאת תמיד בירידה
נכתוב בצורה מתמטית
עלייה : -\sqrt2 < x <0 , x > \sqrt2
ירידה : x<-\sqrt2 , 0<x<\sqrt2
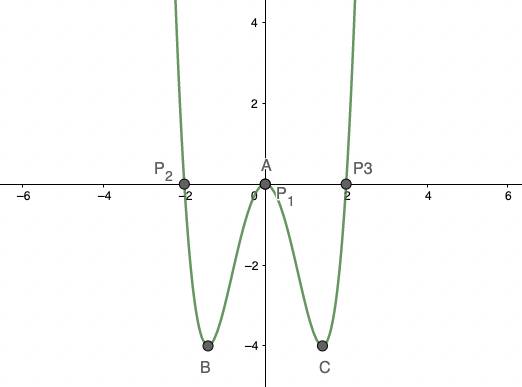
שרטוט גרף לפונקציה:
נוכל כעת לשרטט גרף של הפונקציה בצורה מדוייקת , גרף הפונקציה יראה כך:
חקירת הפונקציה f(x) = \frac{x^2-2x+1}{x}
הפונקציה הזאת מעת שונה מהפונקציות הקודמות, כאן הפעם יש לנו מנה של פונקציות, תחום הגדרה וגם שרטוט הפונקציה שונה לגמרי. בואו נתחיל
מציאת תחום הגדרה:
מאחר והמכנה בפונקציה לא יכול להיות שווה לאפס, תחום ההגדרה הוא לכל x \neq 0
מציאת נק׳ חיתוך עם הצירים:
נשווה את הפונקציה לאפס ונמצא את נקודות החיתוך שלה עם הצירים
f(x) = \frac{x^2-2x+1}{x}
אנחנו יכולים לראות שהמונה הוא בעצם ייצוג של נוסחת הכפל המקוצר הראשונה (תזכורת לנוסחאות הכפל המקוצר)
(a+b)^ = a^2-2ab +b^2
ולכן אפשר לכתוב את הפונקציה גם כך:
f(x) = \frac{(x-1)^2}{x}
ויהיה לנו הרבה יותר קל למצוא את נקודות החיתוך שלה עם הצירים:
\frac{(x-1)^2}{x}=0
בעצם
(x-1)^2=0
לכן יש לנו נקודת חיתוך אחת בלבד עם הצירים
x=1 \rightarrow P(1,0)
נרשום את הנקודה P על מערכת הצירים
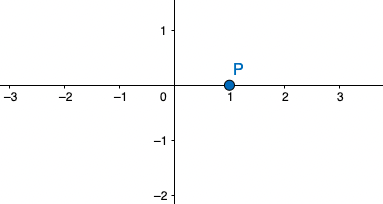
מציאת נקודות קיצון:
נגזור את הפונקציה הזאת, שהיא יותר מסובכת לגזירה ממה שגזרנו עד עתה (תזכורת לחוקי הנגזרת)
y = \frac{f(x)}{g(x)}
אז נגזרת שלה תוגדר ע״י
y’ = \frac{ f'(x)\cdot g(x) – f(x) \cdot g'(x)}{\left [ g(x) \right ]^2}
לכן הנגזרת הראשונה של הפונקציה שלנו היא:
f'(x)=\frac{(x^2-2x+1)^{‘} \cdot x – (x)^{‘} \cdot (x^2-2x+1)}{x^2}
נתחיל בגזירה הזאת
f'(x) = \frac{(2x-2)x – 1(x^2-2x+1)}{x^2} = \frac{2x^2-2x – x^2+2x-1)}{x^2}
נסכם את הנגזרת:
f'(x) = \frac{x^2-1}{x^2}
כעת כדי למצוא את נקודות הקיצון, נשווה את הנגזרת לאפס
למעשה נצטרך להשוות רק את המונה לאפס
x^2-1=0 \rightarrow x^2=1
ולכן יש לנו שתי נקודות החשודות כנקודות קיצון
נקודה ראשונה A
x_1=1 , f(1) =0 \rightarrow A(1,0)
ונקודה שניה B
x_2=-1 , f(-1) =0 \rightarrow B(-1,-2)
נעלה גם את שתי נקודות הקיצון על מערכת הצירים:
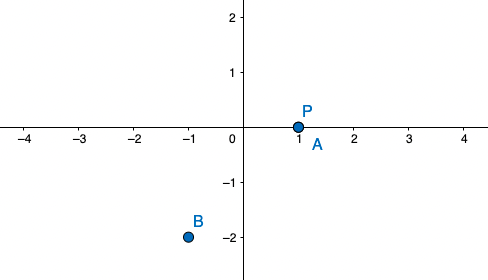
מציאת אופי נקודות הקיצון (מקסימום או מינימום):
נמלא טבלה המכילה את ערכי הנגזרת הראשונה בקרבת הנקודות החשודות כקיצון ונקבע :
נקודת מקסימום, אם אנחנו רואים שערך הנגזרת בסביבת הנקודה החשודה משתנה מחיובי לשלילי (עובר מעליה לירידה)
נקודת מינימום, אם אנחנו רואים שערך הנגזרת בסביבת הנקודה החשודה משתנה משלילי לחיובי (עובר מירידה לעליה)
| 2 | 1 | 0.5 | 0.5- | 1- | 2- | |
| 0.75 | 0 | 3- | 3- | 0 | 0.75 | נגזרת |
| עולה | יורדת | יורדת | עולה | הפונקציה עולה או יורדת | ||
| מינימום | מקסימום | סוג הנקודה |
אנחנו יכולים עכשיו לקבוע את סוג הנקודות:
בנקודה B(-1,-2) עוברים מעלייה לירידה ולכן היא נקודת מקסימום
בנקודה A(1,0) עוברים מירידה לעלייה ולכן היא נקודת מינימום
קביעת תחומי עלייה וירידה:
מתוך הטבלה נוכל לציין את תחומי העלייה והירידה של הפונקציה, אנחנו חייבים לזכור שהפונקציה אינה מוגדרת בנקודה x=0 ולכן יש לה צורה שונה מהפונקציות ״הרגילות״ שהכרנו עד עכשיו
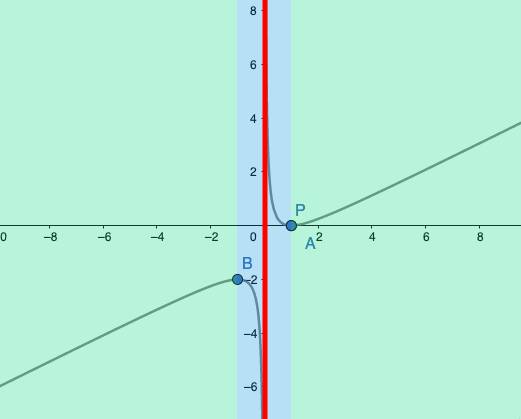
תחומי העליה : x>1 , x< -1
תחומי ירידה : -1 < x < 0 , 0 < x < 1
שרטוט גרף לפונקציה:
נוכל כעת לשרטט גרף של הפונקציה בצורה מדוייקת , גרף הפונקציה יראה כך:
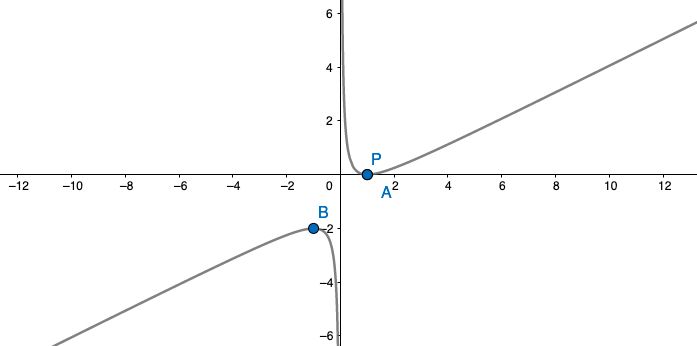
ומה הלאה?
לתרגל ולתרגל!


