אחד הנושאים הראשונים הנלמדים בגאומטריה אנליטית הוא מציאת המרחק בין שתי נקודות, מה שידוע גם כדיסטנס (Distance).
בשיעור הבא נלמד:
- מהי נוסחת המרחק בין שתי נקודות
- נוסחת המרחק – הסבר , הוכחה ודרך
- המרחק בין שתי נקודות – שאלות הצבה (רמה 1)
- המרחק בין שתי נקודות – שאלות עם נעלם אחד (רמה 2)
- מציאת המרחק בין נקודה לישר (בעזרת נוסחת הדיסטנס)
- המרחק בין שתי נקודות – שאלות עם שני נעלמים (רמה 3)
- מחשבון למציאת המרחק בין שתי נקודות
נוסחת המרחק בין שתי נקודות
לפני שניכנס לעומק השיעור, נראה ראשית מהי נוסחאת המרחק בין שתי נקודות:
d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
d מתאר את המרחק שבין שתי הנקודות P_{1}(x_{1},y_{1}) ו P_{2}(x_{2},y_{2})
נוסחת המרחק בין שתי נקודות – הסבר
סרטון הסבר ןפתרון וידאי של שאלות ההצבה 1-3
נרשום על הצירים שתי נקודות, כמו בתרשים הבא:
כעת כשנרצה לחשב את המרחק שבין הנקודות A ו B נשרטט משולש ישר זוווית שהיתר שלו הוא הקטע AB, אותו נוכל לחשב בעזרת משפט פיתגורס:
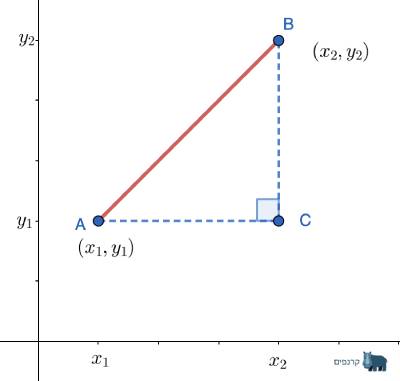
לפי משפט פיתגורס : AB^2=AC^2+BC^2
ולכן אורך הקטע AB הוא:
AB = \sqrt{AC^2+BC^2}כעת נותר לההבין את אורכי הקטעים AC ו BC ולהציבם בנוסחה הנ״ל
אורך הקטע AC הוא הפרש קורדינאטות הנקודות על ציר הx
אורך הקטע BC הוא הפרש קורדינאטות הנקודות על ציר הy
AC=(x_{2}-x_{1})
BC=(y_{2}-y_{1})
כעת נציב בנוסחת פיתגורס ויש לנו את הנוסחה למציאת המרחק בין שתי נקודות
d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
דוגמאות לחישוב המרחק בין שתי נקודות – שאלות הצבה:
מצאו את המרחק שבין הנקודות (0,4) ו (4,7)
פתרון:
נציב את הנקודות בנוסחת הדיסטנס
d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
הצבה
d=\sqrt{(4-0)^2+(7-4)^2}
ראשית
d=\sqrt{(4)^2+(3)^2}
אחר כך
d=\sqrt{16+9}=\sqrt{25}
ולבסןף
d=5
מצאו את המרחק שבין הנקודות (3,5) ו (7-,4-)
פתרון:
נציב את הנקודות בנוסחת הדיסטנס
d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
הצבה
d=\sqrt{(-4-3)^2+(-7-5)^2}
נחשב
d=\sqrt{(-7)^2+(-12)^2}
נפשט
d=\sqrt{49+144}
ונגיע לתוצאה הסופית
d=\sqrt{193}
נעמה יצאה למסלול ריצה , במהלך הריצה עברה נעמה בנקודות המצויינות גרף.
איזה מרחק רצה נעמה
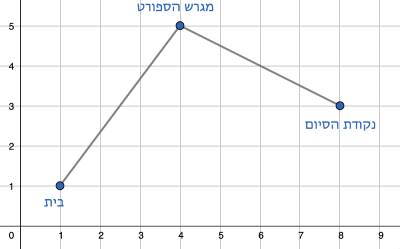
פתרון:
ראשית נמצא את הקורדינאטות של נקודות הציון
- נקודת היציאה הבית נמצאת בנקודה (1,1)
- נקודת האמצע מגרש הספורט נמצאת בנקודה (4,5)
- נקודת הסיום נמצאת בקורדינאטות (8,3)
נחשב תחילה את המרחק אותו עברה נעמה מהבית עד למגרש הספורט
d_{1}=\sqrt{(4-1)^2+(5-1)^2}נציב
d_{1}=\sqrt{(3)^2+(4^2}
נפשט
d_{1}=\sqrt{9+16}=\sqrt{25}
ולבסוף
כעת נחשב את קטע הריצה השני שבין מגרש הספורט לנקודת הסיום, כלומר מ(4,5) ל (8,3)
d_{2}=\sqrt{(8-3)^2+(3-5)^2}נפשט
d_{2}=\sqrt{(5)^2+(2^2}
נסכום
d_{2}=\sqrt{25+4}=\sqrt{29}
ולבסוף
d_{2}=\sqrt{29}
המרחק הכולל אותו עברה נעמה הוא:
d=5+\sqrt{29}דוגמאות לחישוב המרחק בין שתי נקודות – שאלות עם נעלם אחד:
סרטון הסבר ופתרון תרגילים 4 ו 5 בצורה מפורטת:
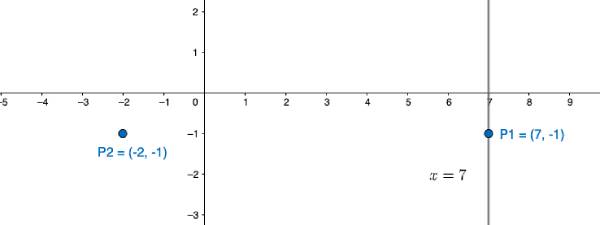
מצא נקודה על ישר x=7 הנמצא במרחק 9 יחידות מהנקודה (1-,2-)
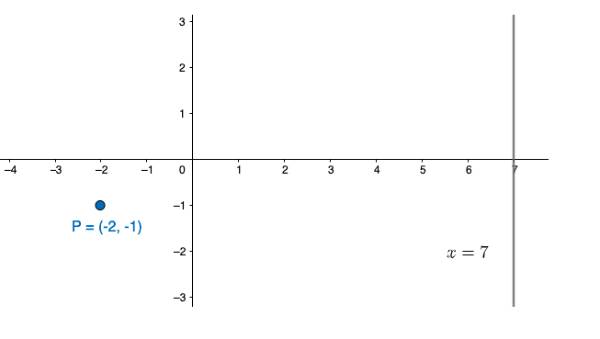
פתרון:
נסמן נקודה על הישר x=7 כך p(7,y)
אנחנו יודעים שהמרחק בין הנקודה p לישר הוא 9 ולכן
d=9 \rightarrow d^2=9^2=81
כעת אפשר להציב את הנתונים בנוסחת המרחק
d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
נעלה אותה בריבוע לשם
d=(x_{2}-x_{1})^2+(y_{2}-y_{1})^2
נגדיר את שתי הנקודות שלנו
p_{1}(-2,-1) ו p_{2}(7,y_{2})
נציב את הנקודות בנוסחה
81=(7–2)^2+(y–1)^2=9^2+(y+1)^2
נחסיר 81 משני האגפים ונקסל
0=(y+1)^2
נוציא שורש לשני האגפים ונקבל
y+1=0 \rightarrow y=-1
לכן הנקודה p תהיה ב
p(7,-1)אפשר לבדוק את התוצאה ע״י מציאת המרחק בין הנקודות
p_{1}(-2,-1) ו p_{2}(7,-1)
נעשה בדיקה מהירה
d=\sqrt{(7–2)^2+(-1–1)^2}=\sqrt{9^2+0^2}=9
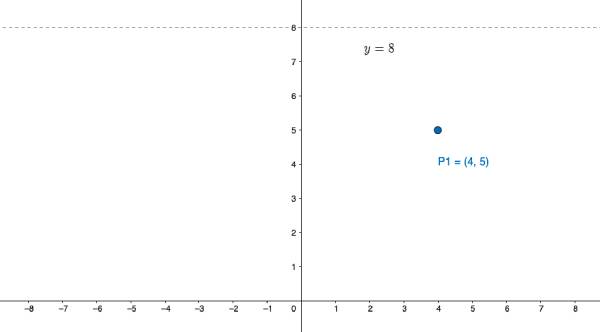
מצאו נקודה הנמצאת על הישר y=8 ובמרחק של 5 יחידות מהנקודה (4,5)
פתרון
בדומה לשאלה הקודמת, נקודה שנימצאת על הישר y=8 תהיה תמיד מהסוג p(x,8)
אנחנו יודעים שהמרחק בין הנקודה p לישר הוא 5 ולכן
d=5 \rightarrow d^2=5^2=25
כעת אפשר להציב את הנתונים בנוסחת המרחק
d=\sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2}
נגדיר את שתי הנקודות שלנו
p_{1}(4,5) p_{2}(x,8)
נציב אותן בנוסחה
5=\sqrt{(x-4)^2+(8-5)^2}
נעלה בריבוע את שני האגפים
25=(x-4)^2+(8-5)^2
ונפשט מעט
25=x^2 -8x + 16 + 9
נצמצם ונגיע למשוואה ריבועית
25 = x^2 – 8x + 25
נחסיר משני האגפים 25 ונקבל את המשוואה הריבועית הבאה:
0 = x^2 – 8x \rightarrow x(x-8)=0
למשוואה שני פתרונות
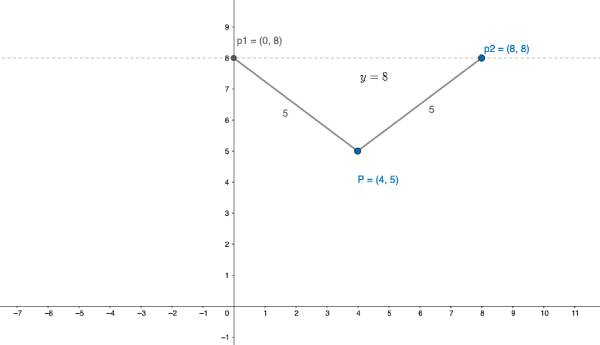
x_{1}=0 x_{2}=8
ולכן לתרגיל שני פרונות שונים
p1_{1}(0,8) p_{2}(8,8)
טיפ – רוצים לבדוק את התוצאה שלכם ולוודא שאתם בסדר? השתמשו במחשבון המרחק בין שתי נקודות שלנו
מצא נקודה על הישר x=4 הנמצאת במרחק שווה מהנקודה 6,2 ומציר ה x
פתרון
נקודה שנמצא על x=4 תהיה מהצורה p(4,t)
המרחק של הנקודה 6,2 מהנקודה p נתונה ע״י המשוואה
d=\sqrt{(6-4)^2 + (2-t)^2}
נעלה בריבוע את שני האגפים
d^2=2^2+(2-t)^2=4+4-4t+t^2
נפשט
d^2=t^2-4t+8המרחק של הנקודה p מציר הx יהיה
d=|t|
נעלה את הרחק בריבוע ונקבל
d^2=t^2
כעת נוכל להשוות בין המרחקים
t^2=t^2-4t+8 / -t^2 -4t
נחסר ונעביר אגפים
4t=8 \rightarrow t=2
לכן הנקודה המחופשת היא
p(4,2)
תרגול מציאת מרחק נקודה מישר בעזרת נוסחאת הדיסטנס:
שימו לב, כאן נחשב את המרחק המינימלי בין נקודה לישר בעזרת שימוש בנוסחאת הדיסטנס, אפשר לחשב את המרחק בעזרת הנוסחה לחישוב מרחק בין נקודה לישר כאן


