תחום הגדרה של פונקציה

בעמוד הזה נלמד :

1. מהי פונקציה בשתי שורות או כמה משפטים:-)
2. מהו תחום הגדרה – המושג באופן כללי
3. מציאת תחום הגדרה של פולינום
4. מציאת תחום הגדרה שלפונקצית מנה או פונקציה רציונלית
5. מציאת תחום הגדרה של פונקציית שורש
6. מציאת תחום הגדרה של פונקציה טריגונומטרית

מהי פונקציה בשתי שורות

אם הגעתם לשיעור הזה, אתם בוודאי כבר יודעים מהי פונקציה, אבל רק לצורך ההבהרה, אפשר לומר שפונקציה היא קופסא כלשהי שלתוכה אנחנו מכניסים מספר והקופסא עושה בו שימוש וביציאה מהקופסה אנחנו מקבלים מספר או ערך אחר, למשל קופסא שלוקחת את המספר שנותנים לה בכניסה ומכפילה אותו ב2, קופסא אחרת תיקח את המספר בכניסה , תעלה אותו בריבוע, תחלק אותו ב2 ותוסיף 8 וכן הלאה…

מה הוא תחום הגדרה של פונקציה?

אמרנו שהפונקציה מקבלת מספר ומוציאה עבורו תוצאה כלשהי, אשר תחום ההגדרה של הפונקציה כולל את כל המספרים שאם נכניס אותם לפונקציה נקבל תוצאה ממשית, כלומר מספר ממש.

מציאת תחום הגדרה של פולינום

פונקציית פולינום היא פונקציית חזקה, דוגמאות לפונקציית חזקה או פולינום הן:
\(f(x) = x^2+4x+5\)
או
\(f(x) = x^12 + 5x^4 – 12x^3 + 6x^2 + 4x -1\)

פונקציית פולינום מגדרת לכל מספר, את תחום ההגדרה הזה אנחנו כותבים כך:
\(x \in\mathbb{R}\)

פירוש

משמעות הסימן \( \in \) נמצא בתוך
משמעות הסימן \(  \mathbb{R}\) הוא משפחת המספרים הרציונלים
אם ננסה לקרוא לעצמנו בקול את מה שכתבנו נאמר, x נמצא בתוך כל המספרים הרציונלים, כלומר אין עליו שום הגבלה

פונקציות פולינום הן הפונקציות הקלות ביותר, בו נתקדם שלב.

מציאת תחום הגדרה שלפונקצית מנה או פונקציה רציונלית

פונקציה רציונלית היא שם יפה יותר לפונקציה שהיא שבר.

מה יכול להיות מיוחד בפונקציות שבר? 

אנחנו יודעים שבמנה כאשר המכנה שווה לאפס התוצאה אינה מוגדרת ולכן אם יש לנו פונקציה שהמכנה שלה שווה לאפס בנקודות מסויימות, היא לא מוגדרת באותן נקודות.

בואו נתחיל עם כמה דוגמאות לתחום הגדרה שלפונקציות שבר:

מהו תחום ההגדרה של הפונקציה \(f(x) = \frac{1}{x}\) ?
שאתי אולי הדוגמה הכי נפוצה איתה מתחילים את הנושא
אנחנו יודעים שהערך במכנה לא יכולים להיות 0 אחרת אין הגדרה לתוצאת השבר, לכן נוכל מיד לומר במילים שתחום ההגדרה של הפונקציה, הוא כל המספרים למעט המספר 0
איך כותבים את תחום ההגדרה בשפה מתמטית?
תחום ההגדרה של הפונקציה הוא עבור כל x למעט \(x \neq 0\)

מהו תחום ההגדרה של הפונקציה \(f(x) = \frac{2x}{(x+1)(x-4)}\)
שימו לב שאנחנו לא מתייחסים למה שקורה במונה, הוא לא מעניין אותנו למטרת מציאת תחום ההגדרה של פונקציית שבר
בשאלה הזאת אנחנו רואים שהמכנה יכול להתאפס בשני המקרים הבאים:
\(x+1 = 0 או x-4=0\)
לכן הפונקציה אינה מוגדרת בנקודות x=4 ו x=-1
נוכל לכתוב את זה בשפה מתמטית כך:
הפונקציה מוגדרת לכל x למעת \(x \neq -1 , x\neq 4\)

חשוב!!! אם ניתן לצמצצם את שבר הפונקציות, את תחום ההגדרה עושים תמיד לפני הצמצום!

מהו תחום ההגדרה של הפונקציה \(f(x) = \frac{2x-4}{(2x-4)(5+x)}\)
כנראה שהדבר הראשון שאנחנו נרצה לעשות הוא לצמצם את השבר, הרי למה לא? אז זהו שלא מצמצמים את השבר למטרת בדיקת תחום הגדרת הפונקציה

אז איך נמצא את תחום ההגדרה של הפונקציה הזאת?
אנחנו צריכים לדאוג שהמכנה לא שווה לאפס, מתי זה קורה?
\((2x-4)(5+x) \neq 0\)
מכאן תחום ההגדרה יהיה
\(2x-4\neq 0 \rightarrow x\neq 2\)
וגם
\(5+x \neq 0 \rightarrow x \neq -5\)

במילים אחרות הפונקציה אינה מוגדרת עבור x=2 ו x=-5

מציאת תחום הגדרה של פונקציית שורש:

כשניגש לפונקציית שורש, ניקח בחשבון שהשולש לא יכול להיות שלילי ולכן בתוך השורש יהיה תמיד ביטוי חיובי או שווה לאפס
נתחיל עם הדוגמה הפשוטה ביותר
מצאו את תחום ההגדרה של הפונקציה \(f()=\sqrt{x}\)
כאמור אנחנו יודעים שפונקציית השורש תחזיר ערך אך ורק אם הערך שבתוכה חיובי, לכן עבור x שלילי הפונקציה לא קיימת, ולכן:
תחום ההגדרה של \(f(x) = \sqrt{x} , x\ge0\)

דוגמה מספר 2
מצאו את תחום ההגדרה של הפונקציה \(f(x)=\sqrt{7x+5}\)
יש לוודא שמה שקורה מתחת שורש תמיד גדול מאפס ולכן, תחום ההגדרה יהיה
\(7x+5\ge0 \rightarrow x\ge\frac{5}{7}\)

דוגמה מספר 3
מצאו את תחום ההגדרה של הפונקציה \(f(x)=\sqrt{\frac{3x-3}{2x+1}}\)
יש לנו שילוב של כמה בדיקות
בדיקה ראשונה, המכנה צריך להיות שונה מ אפס \(2x+1 \neq 0\) ולכן \(x \neq -\frac{1}{2}\)

בדיקה שניה , מה שיש בתוך השורש צריך להיות גדול מאפס, כלומר
\(\frac{3x-3}{2x+1}\ge0\)
חשוב! יש לשים לב שכאן אנחנו חייבים לכפיל את שני האגפים בריבוע המכנה ולא רק במכנה, אנחנו עדין רוצים לשמור על ההשפעה של המכנה על תחום ההגדרה
\((3x-3)(2x+1) \ge0\)
נפתח את נמכפלה ונצמצם, נקבל:
\(2x^2-x-1\ge 0\)
נפתור את המשוואה הריבועית ונמצא את נקודות החיתוך שלה עם הצירים (אפשר להשתמש במחשבון פתרון משוואת השורשים שלנו)

פתרונות המשוואה הם:\(x_1=1 , x_2=-\frac{1}{2}\)

פונקציה ריבועית ״צוחקת״ נראית ככה:

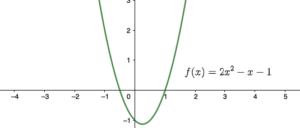
לכן הפונקציה גדולה מאפס מימין לנקודת החיתוך עם ציר הx ומצד שמאל של נקודת החיתוך עם ציר הx
\(x\ge1 , x\le-\frac{1}{2}\) נסכם את תחום ההגדרה של הפונקציה \(x\ge1 , x\le-\frac{1}{2} , x \neq -\frac{1}{2}\)

מציאת תחום הגדרה של פונקציה טריגונומטרית

פונקציות הסינוס והקוסינוס מוגדרות לכל x
פונקציות הטנגנסט והקוטנגנסט מוגדרות אחרת, בואו נראה
\(f(x) = \tan{x} = \frac{\sin x}{\cos x}\)
יש לנו פונקציה שהיא מנה, אנחנו יודעים שהשבר מוגדר כל עוד המכנה שונה מאפס
מתי הקוסינוס מתאפס?
\(\cos(x)=0 \Rightarrow x=\frac{\pi}{2} + n \pi \)
לכן פונקציית טנגנסט מוגדרת עבור כל \(x \neq \frac{\pi}{2} + n \pi\)