משהו משפט פיתגורס?
משפט פיתגורס הוא אחד המשפטים המוכרים בגאומטריה. המשפט אומר שבמשולש ישר זווית סכום ריבועי הצלעות האנכיות שווה לריבוע היתר.
a^{2}+b^{2} = c^{2}הוכחת משפט פיתגורס:
ישנן מאות הוכחות שונות למשפט פיתגורס, יש אפילו ספר שמאגד 368 הוכחות שונות, הנה אחד מהפתרונות מהמוכרים:
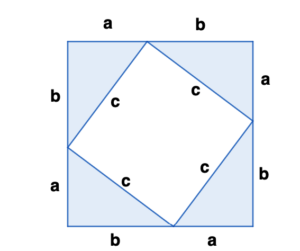
אם ניקח 4 משולשים ישר זווית בעלי שני אנכים a ו b ויתר c.
למעשה קיבלנו שני ריבועים:
ריבוע פנימי שאורך צלעו c
ריבוע חיצוני שאורך צלעו a+b
מכאן אפשר לחשב את השטח של ריבוע הגדול בשתי דרכים ולהגיע לשיוויון פיתגורס, כך:
צד שמאל של המשוואה הוא שטח הריבוע הגדול בעל צלע באורך a+bהמצד שני הוא שטח הריבוע הפנימי בעל צלע באורך c ובנוסף שטח 4 משולשים בעלי אנכים a ו b:
\left ( a+b \right )^{2} = c^{2}+4\cdot \frac{a\cdot b}{2}
נפשט את שני הצדדים:
a^{2}+2\cdot a\cdot b+b^{2} = c^{2} + 2\cdot a\cdot b
כעת נחסיר משני האגפים 2ab ונקבל את משפט פיתגורס, מש״ל:
a^{2}+b^{2} = c^{2}
שימושים למשפט פיתגורס:
אחד השימושים הנפוצים למשפט פיתגרוס הוא מציאת אלכסונים במרובעים ומציאת אורך היתר במשלושים ישרי זווית:
שימוש במשפט פיתגורס לחישוב אורך היתר במשולש ישר זווית:נתון המשולש הבא:
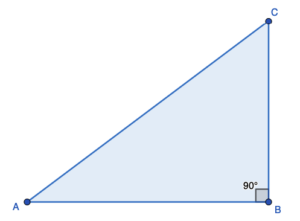נתון כי אורכי הצלעות הם:
BC = 6
AB = 8
- חשבו את אורך היתר (AC) במשולש
- חשבו את שטח המשולש
פתרון:
לחישוב אורך היתר נשתמש במשפט פיתגורס:
Ac^{2} = BC^{2} + AB^{2}
נציב את אורכי הצלעות ונקבל
AC^{2} = 6^{2}+8^{2}=36+64=100
נוציא שורש ונקבל
AC = \sqrt{100} =10
תרגיל 2:
שימוש במשפט פיתגורס לחישוב אורך ניצב טשטח משולש ישר זווית:נתון המשולש הבא, אורכי הצלעות נתונים בשרטוט
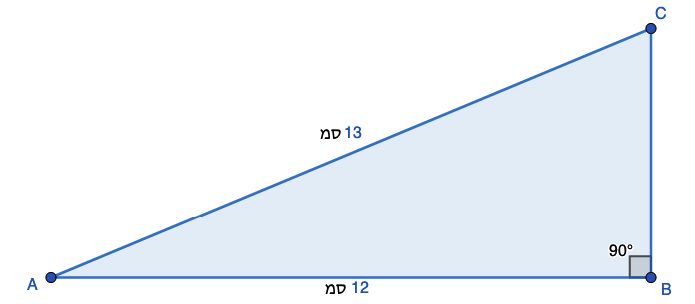
מצאו את אורך הגובה AB וחשבו את שטח משולש ABC
פתרון:
ראשית נחשב לפי משפט פיתגורס את אורך הגובה BC ע״י שימוש במשפט פיתגורס:
AC^{2} = BC^{2} + AB^{2}
נבודד את היתר החסר במשוואת פיתגורס:
BC^{2} = AC^{2} – AB^{2} = 13^{2} – 12^{2} = 169-144
=25
נוציא שורש ונקבל את אורך היתר החסר
BC = \sqrt{25} = 5
כעת נחשב את שטח המשולש לפי:
S = \frac{1}{2}\cdot AB \cdot BC = \frac{1}{2}\cdot12\cdot 5=60
רינה
31 דצמ 2021יש כמה מאות הוכחות שונות למשפט פיתגורס
adminnn3
31 דצמ 2021נכון, נעדכן את הפתיח למאות במקום מעל 10.
אגב, כמה הוכחות מלמדים בכיתתך?
ניק
13 פבר 2025האם אין צורך להוכיח, עוד לפני חישובי השטחים, שהמצולע הפנימי שכל צלעותיו באורך c, הוא ריבוע?
adminnn3
16 פבר 2025היי ניק,
לצורך ההוכחה פה הנחנו שהמרובע הפנימי הוא ריבוע, כן.
כל המשולשים על המסגרת הם חופפים וישר זווית, אם נסמן במשולשים את הזווית הישרה זווית אחת באלפא וזווית שניה בבטא, נקבל ש אלפא+בטא שווה ל90 מעלות
סכום זוויות במשולש פחות 90 מעלות. מכאן כשנסתכל על אחת מהזוויות במרובע הפנימי נקבל שהזווית היא 180 פחות (אלפא+בטא) סכום הזוויות על ישר ולכן היא גם שווה 90 מעלות.
זה לגבי הזוויות
לגבי אורך הצלע, היות והצלעות במרובע הן היתר של משולש וכל המשולשים שווים, אז כל הצלעות a שווות
וכך יש לנו ריבוע.
אולי נעלה סרטון הסבר בקרוב.
תודה!