מציאת נקודת קיצון

העמוד בבניה, התוכן זמין חלקית

בשיעור הזה נעבור על הנושאים הבאים, כולל תרגול, פתרונות מלאי, טיפים ועוד

1. מהי נקודת קיצון
2. איך מחשבים נגזרת
3. מציאת נקודת קיצון ע״י השוואת הנגזרת לאפס
4. קביעה האם נקודת הקיצון היא נקודת מקסימום או מינימום
5. תרגילים
   • חקירת נקודות קיצון של פרבולה עם נקודת קיצון יחידה
   • חקירת נקודות קיצון של פונקציה ממעלה שלישית עם שתי נקודות קיצון
   • חקירת נקודות קיצון של פונקציה ממעלה רביעית עםשלוש נקודות קיצון

מהי נקודת קיצון בכלל?

נקודת קיצון היא נקודה שגבוהה או נמוכה משתי נקודות בסביבה שלה.

יש שני סוגים של נקודות קיצון:

1. נקודת מקסימום – זאת נקודה שבה ערך הפונקציה גדול יותר מערך הפונקציה בסביבה הקרובה שלה ( מימין ונשמאל )
2. נקודת מינימום – זאת נקודה שבה ערך הפונקציה קטנה יותר מערך הפונקציה בסביבה הקרובה שלה ( מימין ונשמאל )

נתבונן בגרפים הבאים:

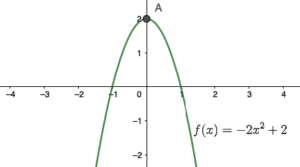
נקודת מקסימום ערך הפונקציה בנקודה A גבוה מערך הפונקציה בכל הנקודות האפשריות, כלומר אפשר לומר ש \(f(x_A)>f(x) \) לכל \(x\neq x_A\) לכן נקודה A תיקרא נקודת המקסימום של הפונקציה

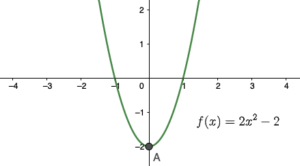
נקודת מינימום ערך הפונקציה בנקודה A נמוך מערך הפונקציה בכל הנקודות האפשריות, כלומר אפשר לומר ש \(f(x_A)<f(x) \) לכל \(x\neq x_A\) לכן נקודה A תיקרא נקודת המינימום של הפונקציה

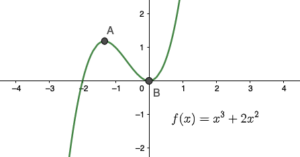
נקודות מקסימום ומינימום באותה הפונקציה לפונקציה שתי נקודות קיצון, נקודות קיצון מקומיות. אנחנו רואים שבנקודה A ערך הפונקציה גדול מהערכים שבסביבה הקרובה לנקודה A, לכן היא נקודת מקסימום לעומת זאת, בנקודה B ערך הפונקציה קטן מהערכים שבסביבה הקרובה לנקודה B, לכן היא נקודת מינימום

לסיכום:

כאשר אנחנו ״הולכים״ על הגרף משמאל לימין ( ערכי ה-x גדלים )

• נקודת מקסימום – היא נקודה שבה ערך הפונקציה עובר מעליה לירידה. הנקודה גבוהה מהסביבה שלה.
• נקודת מינימום – היא נקודה שבה ערך הפונקציה מירידה מעליה לעליה. הנקודה נמוכה מהסביבה שלה.

איך מחשבים נגזרת?

אנחנו נעבור על הנגזרת בקצרה. את הפונקציה גוזרים בצורה הבאה (לדוגמא הזאת אנחנו משתמשים בחזקה מקסימלית של 3) :

\(f(x) = ax^3+bx^2+cx+d\)
נגזרת הפונקציה יסומן כך
\(f'(x) = 3ax^2 + 2bx + c + 0\)

דוגמאות קצרות לחישוב הנגזרת
שאלה 1
מה היא הנגזרת של הפונקציה
\(f(x) = 4x^2 + 2x + 1\)
פתרון
\(f'(x) = 2 \cdot 4x + 2 + 0 = 8x + 2\)

שאלה 2
מה היא הנגזרת של הפונקציה
\(f(x) = 3x^3 – x^2 + 1\)
פתרון
\(f'(x) = 3 \cdot 3x 2 + 0 = 9x – 2\)

 

מציאת נקודות קיצון ע״י השוואת הנגזרת לאפס

התהליך למציאת נקודות קיצון הוא כזה

1. נגזור את הפונקציה
2. נשווה את פונקציית הנגזרת לאפס ונמצא את ערכי ה-x בנקודות חשודות כנקודות קיצון
3. נציב את נקודות הx הללו בפונקציה המקורית ונקבל את ערכי הפונקציה בנקודות הקיצון

קדימה דוגמאות:

קביעה האם נקודת הקיצון היא נקודת מקסימום או מינימום

אחרי שאנחנו יודעים כבר איך למצוא מהי נקודת קיצון, כעת אנחנו צריכים לקבוע האם:

1. נקודת קיצון היא נקודת מקסימום או נקודת מינימום
2. במידה ויש יותר מכמה נקודות קיצון, נצטרך לקבוע מי מהן נקודת מקסימום ומי מהין נקודת מינימום.

יש כמה דרכים לקבוע את סוג נקודת הקיצון

1. הצבה בטבלה וחשיפת ההסביבה של נקודת הקיצון (הדרך הנפוצה יותר).
2. מציאת ערך הנגזרת השניה בנקודת הקיצון.

תרגילים לחקירת נקודות קיצון

לצורך הדגמת התהליך, נתחיל במציאת נקודת הקיצון וסוגה עבור פונקציה מסדר שני, פרבולה, שלה כאמור יש רק נקודת קיצון אחת.

חקירת נקודת קיצון של פרבולה (נקודת קיצון אחת)

נתונה הפרבולה הבאה:

\(f(x) = -x^2 + 2x + 1\)
מצאו את נקודת הקיצון שלה וקבעו האם היא נקודת מקסימום או מינימום

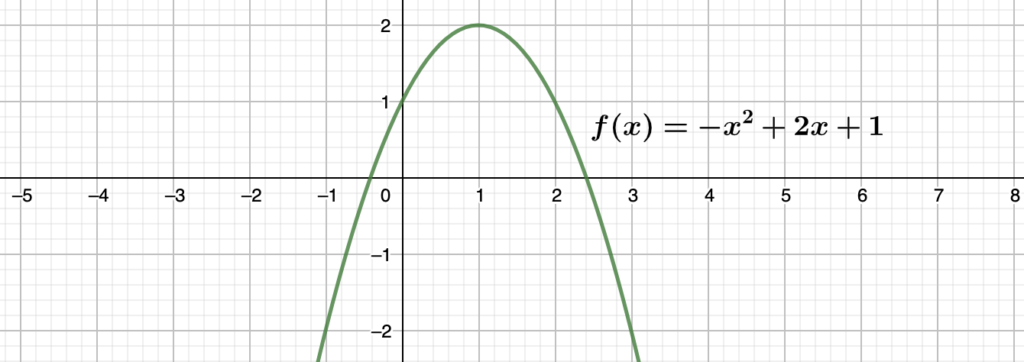
פתרון
ראשית אנחנו יכולים לראות מיד משטוט הפרבולה הנתון שנקודת הקיצון היא נקודת מקסימום
את הקביעה הצאת ניתן להשיג מיד לפי ערכו של המקדם a , המקדם שנמצא איבר הריבועי בפונקציה:

אם a>0 יש לנו פרבולה צוחקת ולכן נקודת הקיצון היא נקודת מינימום

אם a<0 יש לנו פרבולה בוכה ולכן נקודת הקיצון היא נקודת מקסימום (כמו בדוגמא שלנו)

בואו נתחיל:

בשלב הראשון נמצא את נקודת הקיצון, לשם כך נגזור את הפונקציה

\(f(x) = -x^2 + 2x + 1 \rightarrow f'(x)=-2x + 2\)
עכשיו כשנתונה לנו הנגזרת, נשווה אותה ל0 ונמצא את ערכו של x בנקודת הקיצון
\(f'(x)=-2x + 2 = 0\)
נעביר אגפים ונפתור
\(-2x=-2\)
מכאן, בנקודת הקיצון
\(x=1\)

כעת נציב את ערכו של x בפונקציה ונמצא את ערכה בנקודת הקיצון
\(f(1) = -x^2 + 2x + 1=-1^2 + 2\cdot1+1 = -1+2+1=2\)

קביעה האם נקודת הקיצון היא מסוג מקסימום או מינימום
דרך ראשונה ערכה של הנגזת השניה בנקודת הקיצון

• נקודת מקסימום אם \(f”(x)<0\)
• נקודת מינימום אם \(f”(x)>0\)

נחשב את הנגזרת השניה ע״י גזירת של הנגזרת הראשונה
\(f'(x)=-2x + 2 = 0 \rightarrow f”(x)=-2\)
מאחר וערך הנגזרת השניה קבוע -2 ואינו תלוי בx כלשהו
אנחנו יודעים מיד שנקודת הקיצון שלנו היא מסוג מקסימום ונמצאת בנקודה \((1,2)\)

דרך שניה – קביעת סוגה של נקודת הקיצון לפי טבלה

נחשב את ערך הפונקציה ב3 נקודות

1. נקודה ראשונה תהיה נקודת הקיצון עצמה
2. נקודה שניה תהיה נקודה כלשהי לשמאלה של נקודת הקיצון, x שקטן מx בנקודת הקיצון (במקרה הזה x=0)
3. נקודה שלישית תהיה נקודה כלשהי לימינה של נקודת הקיצון, x שגדול מx בנקודת הקיצון (במקרה הזה x=2)

נבנה טבלה כמו הדוגמה הזאת

2	1	0	\(x\)
1	2	1	\(f(x)=-x^2+2x+1\)

 

מתוך הטבלה אנחנו יכולים לראות בבירור שערכה של הפונקציה בנקודה x=1 גדול מערכה של הפונקציה בשתי נקודות קרובות משני צידיה של נקודת הקיצון ולכן נקבע שנקודת הקיצון היא נקודת מקסימום

חקירת נקודות של פונקציה ממעלה שלישית (שתי נקודות קיצון)

נתונה הפונקציה הבאה

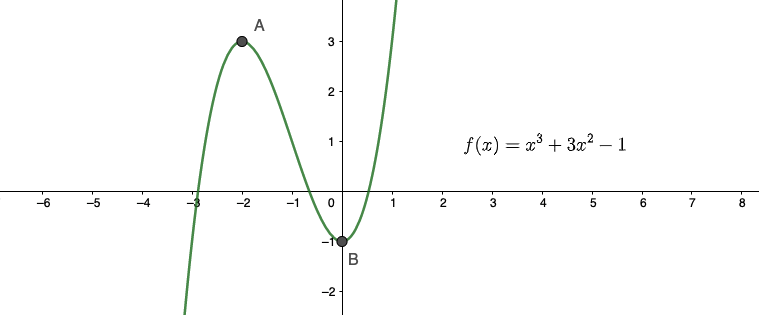
כמו תמיד ניגש ראשית למציאת נקודות הקיצון. אנחנו רואים מיד מתוך גרף הפונקציה שיש לנו כאן שתי נקודות קיצון

שלב ראשון, נגזור את הפונקציה, עפם ראשונה למציאת נקודות הקיצון ובפעם השניה שתהיה לנו עבור הקביעה אם מדובר בנקודות מקסימום או מינימום
\(f(x)=x^3+3x^2 -1\)
נגזרת ראשונה תהיה
\(f'(x)=3x^2+2\cdot3x = 3x^2 + 6x\)
נגזרת שניה תהיה
\(f”(x)=6x+6\)

נמשיך למציאת נקודות הקיצון עצמן, נשוואה את הנגזרת הראשונה לאפס ונמצא את ערכי הx
\(f'(x)=3x^2 + 6x=0\)
מכאן
\(3x^2 + 6x=0 \rightarrow 3x(x+2)=0\)
למשוואה הזאת שני פתרונות
\(x_1=0 , x_2=-2\)

לאחר שמצאנו את ערכי ה x שבהם יש לנו נקודות קיצון, נמצא את ערכי הפונקציה המתאימים
\(x_1 \rightarrow f(0)=0^3 + 3\cdot0^2 -1 = -1\)
\(x_2 \rightarrow f(-2) = (-2)^3 + 3\cdot(-2)^2 -1 = 3\)
לסיכום, שתי נקודות הקיצון הן
\((0,-1),(-2,3)\)

כעת נקבע מי מהן נקודת מקסימום ומי נקודת מינימום
נתחיל בנקודה \((0,-1)\)
נציב 0 בנגזרת השניה
\(f”(0)=6x+6 = 6\)
ולכן מכיוון שנגזרת השניה חיובית הנקודה \((0,-1)\) היא נקודת מינימום (מה שמסתדר גם עם הסרטוט)

כעת נבחן את הנקודה \((-2,3)\)
נציב -2 בנגזרת השניה
\(f”(-2)=6x+6 = -12+6=-6\)
ולכן מכיוון ערך הנגזרת השניה בנקודה היא שלילית, הנקודה \((-2,3)\) היא נקודת מקסימום, מה שמסתדר לנו עם הגרף

לסיכום
\((-2,3)\) נקודת מקסימום
\((0,-1)\) נקודת מינימום

כעת נוודא את התוצאה ע״י בדיקת הצבה בטבלה

1	0	-1	-2	-3	\(x\)
3	-1	1	3	-1	\(f(x)=x^3+3x^2 -1\)

ובכן אנחנו רואים מתוך הטבלה כי:

ערך הפונקציה בנקודה x=-2 גדול מערך הפונקציה בנקודות x=-3 ו x=-1 ולכן היא נקודת מקסימום

ערך הפונקציה בנקודה x=0 קטן מערך הפונקציה בנקודות x=-1 ו x=1 ולכן היא נקודת מינימום

 

חקירת נקודות של פונקציה ממעלה רביעית עם שלוש נקודות קיצון

חקרו את הפונקציה הבאה
\(f(x)=x^4 – x^3 – 2x^2 +1\)
מצאו נקודות קיצון וקבעו מי מהן נקודת מקסימום ומי נקודת מינימום

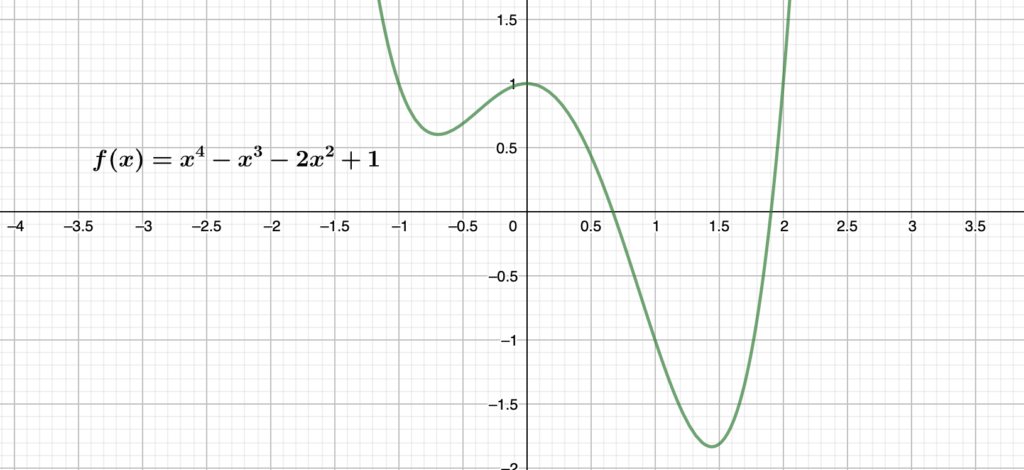
פתרון
נגזור את הפונקציה פעם אחת, נשווה לאפס ונמצא את ערכי הx של נקודות הקיצון
\(f'(x)=4x^3-3x^2-2\cdot2 x = 4x^3-3x^2-4x \)
לאחר הגזירה נשווה ל 0 ונמצא את הנקודות בהן יש לנו קיצון
\(f'(x)=4x^3-3x^2-4x = 0\)
מתחיל בפישוט הנגזרת השניה
\(4x^3-3x^2-4x = 0\)
נוציא x כגורם משותף
\(x(4x^2-3x-4)=0\)
הx שמחוץ לסוגריים מאפס את המשווה כשהוא שווה ל 0
\(x_1=0\)

את יתר הפתרונות נמצא ע״י פתרון המשוואה הריבועית
\(4x^2-3x-4 = 0\)
בעזרת מחשבון השורשים שלנו נמצא שפתרונות המשוואה הם
\(x_2=1.44\) ו \(x_3=-0.69\)
משמצאנו את ערכי הx של נקודות הקיצון נחשב את ערכי הפונקציה בנקודות הקיצון
נציב בפונקציה את ערכי הx בנקודות הקיצון
\(f_1(x_1=0) = 1\)
\(f_2(x_2=1.44) = -1.8\)
\(f_3(x_3=-0.68) = 0.6\)

הנה נקודות הקיצון שלנו
\(P_1(0,1) , P_2(1.44,-1.8) , P_3(-0.68,0.6)\)

נקבע את סוג נקודות הקיצון ע״י בחינת ערך הנגזרת השניה

כאמור כדי לדעת את אופי נקודת הקיצון, נציב את ערך הx בנגזרת השניה
נגזרת שניה חיובית בנקודת קיצון תסמן נקודת מינימום
נגזרת שניה שלילית בנקודת קיצון תסמן נקודת מקסימום

נגזור את הפונקציה פעם נוספת
\(f”(x) = 3\cdot4x^2 – 2\cdot 3x -4 = 12x^2 – 6x – 4\)
\(f”(x) = 12x^2 – 6x – 4\)

כעת כדי לדעת את אופי נקודת הקיצון, נציב את ערך הx בנגזרת השניה
נגזרת שניה חיובית בנקודת קיצון תסמן נקודת מינימום
נגזרת שניה שלילית בנקודת קיצון תסמן נקודת מקסימום

נתחיל עם נקודה \(P_1(0,1)\)
\(f”(0) = 12x^2 – 6x – 4 = -4\)
לכן נקודה P1 היא נקודת מקסימום מקומית

נמשיך לנקודה \(P_2(1.44,-1.8)\)
\(f”(1.44) = 12x^2 – 6x – 4 = 12.24\)
לכן נקודה P2 היא נקודת מינימום מקומית

נסיים עם נקודה \(P_3(-0.68,0.6)\)
\(f”(-0.68) = 12x^2 – 6x – 4 = 5.62\)
לכן נקודה P3 היא נקודת מינימום מקומית

 

נקבע את סוג נקודות הקיצון ע״י בניית טבלת הצבות

2	1.44	1	0	-0.5	-0.68	-1	\(x\)
1	-1.8	-1	1	0.875	0.6	1	\(f(x)=x^4 – x^3 – 2x^2 +1\)

הטבלה מאששת את התוצאות הקודמות