בשיעור הבא נעבור על סוגי הזוויות שבין שני ישרים מקבילים. יש לציין ששמות בצמדי הזוויות נכון גם אם הישרים אינן מקבילים, אולם כאשר הישרים מקבילים, יש לצמדי הזוויות כמה תכונות מעניינות מאוד.
לנוחותכם נוסחאון גרפי המסכם את סוגי הזווית שבין שני ישרים מקבילים
סוגי זוויות בין שני ישרים מקבילים
זוויות מתאימות
זוויות מתחלפות
זוויות מתחלפות פנימיות
זוויות מתחלפות חיצוניות
זוויות חד צדדיות
זוויות חד צדדיות פנימיות
זוויות חד צדדיות חיצוניות
זוויות משלימות
זוויות קודקודיות
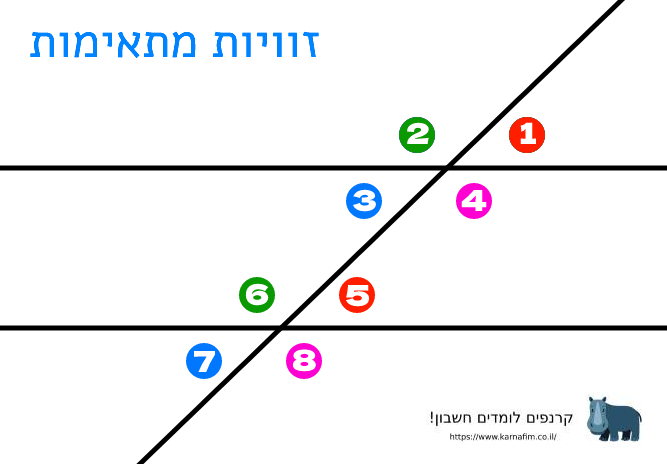
זוויות מתאימות:
זוויות מתאימות נמצאות באותו הצד הישר החותך, ובאותו המפלס של הישרים. אם הישרים מקבילים ערך צמד זוויות מתאימות שווה. אם ערכו של צמד זוויות מתאימות אינו שווה, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות מתאימות:
\angle 1 = \angle 5
\angle 2 = \angle 6
\angle 3 = \angle 7
\angle 4 = \angle 8
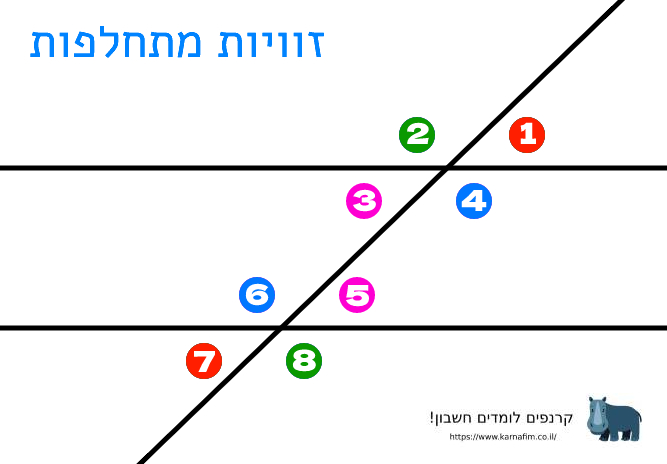
זוויות מתחלפות:
זוויות מתחלפות נמצאות משני צידיו של הישר החותך, אך לא באותו המפלס של הישרים. אם הישרים מקבילים גודל הזוויות המתחלפות שווה. אם ערכן של צמד זוויות מתחלפות אינו שווה, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות מתחלפות:
\angle 1 = \angle 7
\angle 2 = \angle 8
\angle 3 = \angle 5
\angle 4 = \angle 6
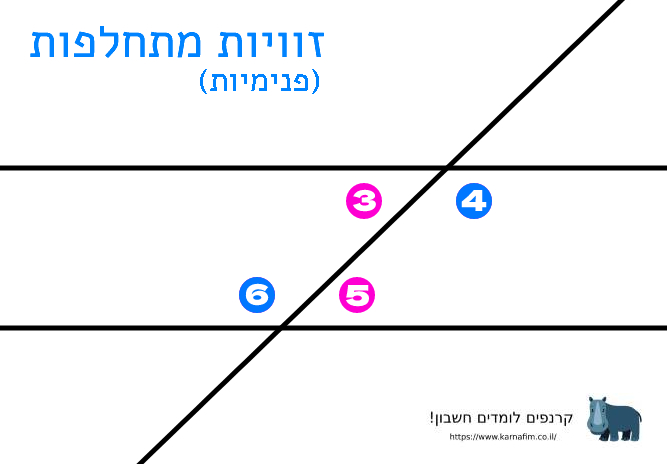
זוויות מתחלפות פנימיות:
זוויות מתחלפות פנימיות נמצאות משני צידיו של הישר החותך, אך לא באותו המפלס של הישרים. אם הישרים מקבילים ערך צמד זוויות מתחלפות חיצוניות שווה שווה. אם ערכןושל צמד זוויות מתחלפות חיצוניות אינו זהה, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות מתחלפות פנימיות:
\angle 3 = \angle 5
\angle 4 = \angle 6
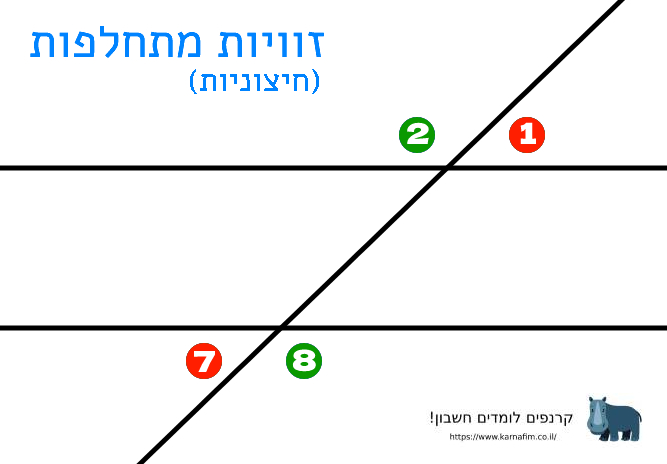
זוויות מתחלפות חיצוניות:
זוויות מתחלפות חיצוניות נמצאות משני צידיו של הישר החותך, אך לא באותו המפלס של הישרים. אם הישרים מקבילים ערכן צמד זוויות מתחלפות חיצוניות שווה. אם ערכן של צמד זוויות מתחלפות חיצוניות שווה אינו שווה, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות מתחלפות חיצוניות:
\angle 1 = \angle 7
\angle 2 = \angle 8
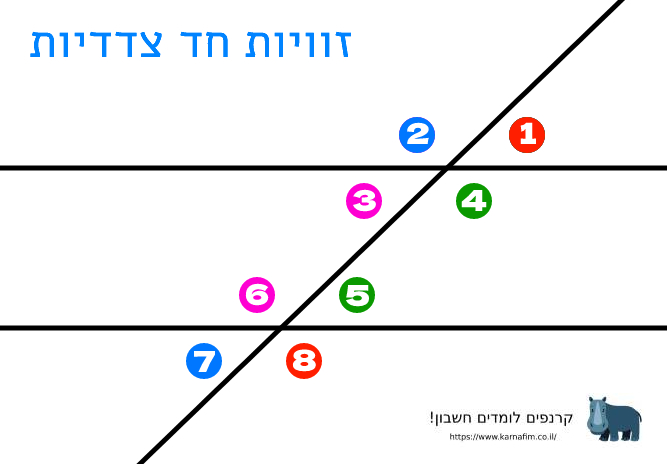
זוויות חד צדדיות:
זוויות חד צדדיות נמצאות באותו הצד של הישר החותך, אך לא באותו המפלס של הישרים. אם הישרים מקבילים סכום צמד הזוויות החד צדדיות שווה ל180 מעלות. אם סכום ערכן של שתי זוויות חד צדדיות אינו 180 מעלות, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות חד צדדיות:
\angle 1 + \angle 8 = 180 ^ֿ \circ
\angle 2 + \angle 7 = 180 ^ֿ \circ
\angle 3 + \angle 6 = 180 ^ֿ \circ
\angle 4 + \angle 5 = 180 ^ֿ \circ
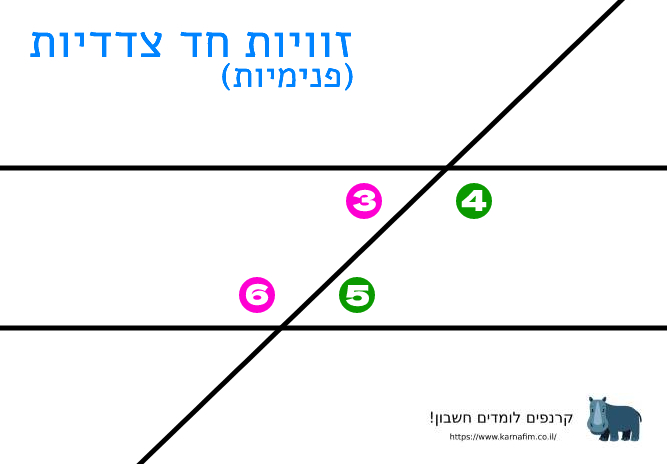
זוויות חד צדדיות פנימיות:
זוויות חד צדדיות פנימיות נמצאות באותו הצד של הישר החותך, אך לא באותו המפלס של הישרים. אם הישרים מקבילים סכום צמד הזוויות החד צדדיות הפנימיות שווה ל180 מעלות. אם סכום ערכן של שתי זוויות החד צדדיות פנימיות אינו 180 מעלות, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות חד צדדיות פנימיות:
\angle 3 + \angle 6 = 180 ^ֿ \circ
\angle 4 + \angle 5 = 180 ^ֿ \circ
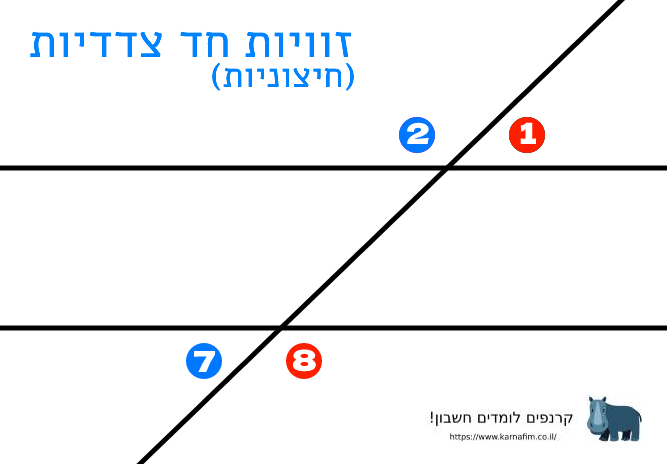
זוויות חד צדדיות חיצוניות:
זוויות חד צדדיות חיצוניות נמצאות באותו הצד של הישר החותך, אך לא באותו המפלס של הישרים. אם הישרים מקבילים סכום צמד הזוויות החד צדדיות חיצוניות שווה ל180 מעלות. אם סכום ערכן של שתי זוויות החד צדדיות חיצוניות אינו 180 מעלות, הישרים אינם מקבילים.
למשל הצמדים הבאים הם צמדי זוויות חד צדדיות פנימיות:
\angle 1 + \angle 8 = 180 ^ֿ \circ
\angle 2 + \angle 7 = 180 ^ֿ \circ
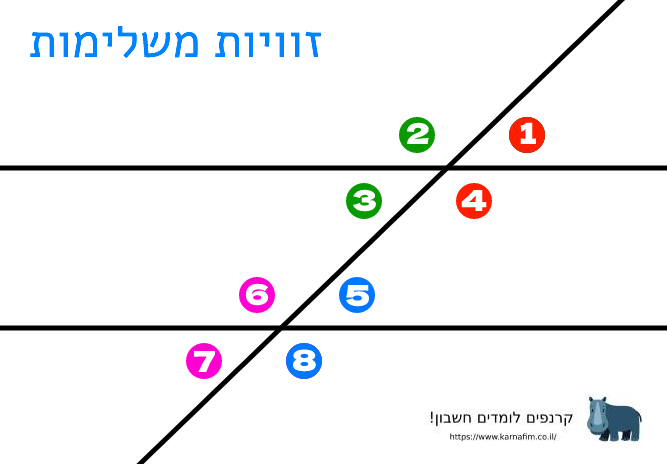
זוויות משלימות:
זוויות משלימות נמצאות על אותו הישר משני צדדיו של ישר חותך. סכום שתי זוויות משלימות הוא 180 מעלות. אם סכומן אינו 180, אז מעורבים יותר משני ישרים
למשל הצמדים הבאים הם צמדי זוויות משלימות:
\angle 1 + \angle 4 = 180 ^ֿ \circ
\angle 2 + \angle 3 = 180 ^ֿ \circ
\angle 5 + \angle 8 = 180 ^ֿ \circ
\angle 6 + \angle 7 = 180 ^ֿ \circ
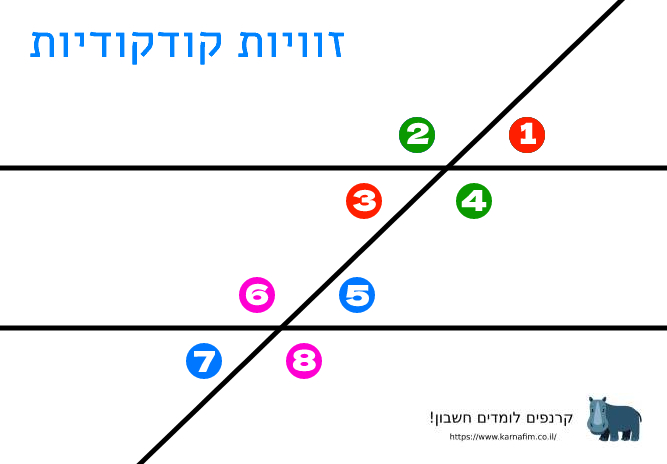
זוויות קודקודיות:
זוויות קודקודיות נמצאות בנקודת החיתוך של שני ישרים, זו מול זו. זוויות קודקודיות שוות זו לזו. במידה ושתי זוויות זו מול זו אינן שוות בגודלן, ישנם יותר משני ישרים מעורבים.
למשל הצמדים הבאים הם צמדי קודקודיות:
\angle 1 = \angle 3
\angle 2 = \angle 4
\angle 5 = \angle 7
\angle 6 = \angle 8