תחומי עלייה וירידה של פרבולה

בעמוד הבא נלמד :

1. ההגדרה של תחום עלייה וירידה
2. מציאת תחום עליה וירידה של פרבולה
3. תרגול מציאת תחומי עלייה וירידה של פרבולה

תחום עלייה וירידה של פרבולה:

תחום עלייה של פונקציה או פרבולה

תחום העלייה של פונקציה או פרבולה יוגדר כאשר ערך הפונקציה f(x) עולה או גדל כאשר ערכו של x עולה, כלומר הערך של הפונקציה עולה ככל שהולכים ״ימינה״ על ציר ה-x.

תחום ירידה של פונקציה או פרבולה

תחום הירידה של פונקציה או פרבולה יוגדר כאשר ערך הפונקציה f(x) ירד או קטן כאשר ערכו של x עולה, כלומר הערך של הפונקציה יורד ככל שהולכים ״ימינה״ על ציר ה-x.

 

מציאת תחומי עלייה ורידה של פרבולה:

נתגרל את מציאת תחומי העליה והירידה שלפרבולה או פונקציה מדרגה שניה בשתי שיטות עיקריות המתאימות להתקדמות בידע, דרך ראשונה מציאת תחומי העליה והירידה מתוך מציאת ערך x בנקודת הקודקוד ודרך שניה ע״י גזירה. את הדוגמה נעשה ע״י חקירת הפונקציה הבאה

\(f(x)=x^2+2x+2\)

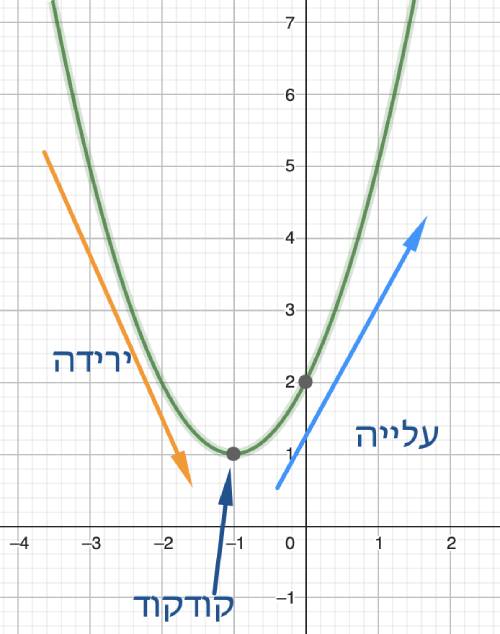
מציאת תחום עלייה וירידה של פרבולה לפי מציאת הקודקוד

ראשית נמצא את נקודת הקודקוד (דף עבודה לתרגול מציאת קודקוד הפרבולה) ע״י שימוש בנוסחה:

\(X_{קודקוד}=-\frac{b}{2a}\)

במקרה שלנו הפונקציה היא

\(f(x)=x^2+2x+2\)

ומקדמיה הם a=1,b=2,c=2, נציב אותם בנוסחה למציאת הקודקוד ונקבל

\(X_{קודקוד}=-\frac{b}{2a}=-\frac{2}{2}=-1\)
כעת משמצאנו את ערך הx בקודקוד הפרבולה, נוכל לראות שהפרבולה היא פרבולה צוחקת מכיוון שמקבל האיבר הריבועי חיובי ולכן הפרבולה עולה בכל התחום שמימין לx בקודקוד ויורדת בכל x שנמצא משמאל לקודקוד, ונוכל לרשום:

תחום עלייה: x>-1

תחום ירידה: x<-1

נוכל לאשר זאת ע״י שימוש בטבלה ובה נציב נקודה משמאל ומימין לנקודת הקודקוד ובדיקת מהו ערך הפרבולה בנקודות האלה:

0	1-	2-	x
2	1	2	f(x)

• בדיקת תחום ירידה: אנחנו רואים שכערך הx גדל מ- 2- ל1- ערך הy יורד מ2 ל1 ולכן הפונקציה למעשה בתחום הירידה שלה.
• בדיקת תחום עלייה: את אותה הבדיקה נעשה גם מצידה השני של נקודת הקודקוד, אנחנו רואים שכאשר ערך הx שאנחנו מודדים עולה מ1- ל0 ערך הפונקציה עולה מ1 ל2 ולכן זהו תחום שבו הפונקציה עולה.

מציאת תחום עלייה וירידה של פונקציה ע״י נגזרת

חקירת מקרה הפרבולה הוא יחסית נוח לפיתרון ע״י גזירה,

חקירת תחומי עלייה וירידה של פונקציה מסדר שלישי

נביט בפונקציה הבאה:

\(f(x)=4x^+3x^2-6x+1\)
מטעמי נוחות נצרף כאן את שרטוט הפונקציה

השלבים שאותם נבצע כדי למצוא את תחומי העליה והירידה של הפונקציה (הסדר הזה נכון לפונקצייות מכל סדר):

1. גזירת הפונקציה
2. השוואת הנגזרת לאפס ומציאת ערכי הx שמאפסים את הנגזרת, אלה יהיו ערכי הx בהם ישנם נקודות קיצון
3. בניית טבלה ובה נשים את ערכי הx בהם נקודות קיצון ונשמור מקום גם לערכים בניהם
4. עבור אותם הערכים נמצא את סימן הנגזרת בנקודה, אין צורך לחשב את ערך הנגזרת אלא רק לדעת אם ערך הנגזרת בנקודות הביניים הוא חיובי או שלילי.
   1. אם ערך הנגזרת הוא שלילי אנחנו נמצאים בתחום ירידה
   2. אם ערך הנגזרת הוא עליה אנחנו נמצאים בתחום עליה
5. שרטוט סקיצה של הפונקציה במידת הצורך.

בואו נעבור על השלבים עם הדוגמה הנ״ל:

\(f(x)=4x^+3x^2-6x+1\)